Cho hình chóp SABC, vuông cân tại A, S A ⊥ A B C , B C = a , S B C , A B C = 45 ° . Trên tia đối của tia SA lấy điểm R sao cho R S = 2 S A . Tính V R . A B C .
A. a 3 8
B. a 3 12
C. a 3 4
D. a 3 24
cho hình chóp SABC có tam giác ABC vuông cân tại A, AB=a, tam giác SAB cân tại S. (SAB) vuông góc với (ABC). (SBC) tạo với đáy 1 góc 45°. Tính thể tích SABC
cho hình chóp SABC có đáy ABC là tam giác vuông cân tại C, BC=a. Hình chiếu vuông góc của S lên mặt phẳng ABC là trung điểm H của cạnh AB, biết rằng SH=2a. Tính theo a thể tích khổi chóp và khoảng cách từ điểm B đế (MAC) với M là trung điểm SB
/hoi-dap/question/31869.html
bạn tham khảo coi
cho hình chóp SABC có SA=a, SA vuông góc với (ABC). Tam giác ABC vuông cân tại B và AB=a, kẻ AH vuông góc với SC tại H. VSABH là
\(\dfrac{V_{SABH}}{V_{SABC}}=\dfrac{SH}{SC}=\left(\dfrac{SA}{SC}\right)^2\Rightarrow V_{SABN}=\left(\dfrac{SA}{SC}\right)^2.V_{SABC}\)
\(AC^2=AB^2+BC^2=2AB^2=2a^2\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\Rightarrow V_{SABH}=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{9}\)
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=BC=a\(\sqrt{3}\) , SAB=SCB=90\(^o\) và khoảng cách từ A đến (SBC) bằng a\(\sqrt{2}\) . Tính diện tích mặt cầu ngoại tiếp hình chóp SABC theo a
Lời giải:
Gọi $H$ là chân đường cao kẻ từ $S$ xuống mặt phẳng $(ABC)$
Ta có \(\left\{\begin{matrix} SH\perp AB\\ SA\perp AB\end{matrix}\right.\Rightarrow AB\perp (SHA)\rightarrow AB\perp HA\)
Tương tự \(BC\perp HC\). Kết hợp với \(ABC\) vuông cân tại $B$ suy ra \(ABCH\) là hình vuông
Có \(AH\parallel (SBC)\Rightarrow d(A,(SBC))=d(H,(SBC))\)
Kẻ \(HT\perp SC\). Có \(\left\{\begin{matrix} SH\perp BC\\ HC\perp BC\end{matrix}\right.\Rightarrow BC\perp (SHC)\Rightarrow BC\perp HT\)
Do đó \(HT\perp (SBC)\Rightarrow d(H,(SBC))=HT=\sqrt{\frac{SH^2.HC^2}{SH^2+HC^2}}=\sqrt{\frac{SH^2.AB^2}{SH^2+AB^2}}=\sqrt{2}\Rightarrow SH=\sqrt{6}a\)
Từ trung điểm $O$ của $AC$ dựng trục vuông góc với mặt phẳng $(ABC)$. Trên trục đó ta lấy điểm $I$ là tâm mặt cầu ngoại tiếp.
\(IS^2=IA^2=IH^2\Leftrightarrow (\overrightarrow{IO}+\overrightarrow{OH}+\overrightarrow{HS})^2=IO^2+OH^2\)
\(\Leftrightarrow HS^2+2\overrightarrow{IO}.\overrightarrow{HS}=0\)
Do \(\overrightarrow {SH}\parallel \overrightarrow {IO}\Rightarrow \overrightarrow {IO}=k\overrightarrow{SH}\). Thay vào PT trên có $k=\frac{1}{2}$
\(\Rightarrow IO=\frac{\sqrt{6}a}{2}\Rightarrow IA=\sqrt{IO^2+AO^2}=\sqrt{3}a\)
\(\Rightarrow S_{\text{mặt cầu}}=4\pi R^2=12a^2\pi\)
cho hình chóp SABC có đáy tam giác ABC vuông cân tại A, AB=a, SC vuông góc với đáy, SC=a, Mặt phẳng (P) qua C và vuông góc với SB cắt SB tại F và cắt SA tại E. Tính VSCEF
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Tính bán kính r của mặt cầu ngoại tiếp hình chóp SABC.
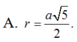
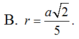
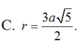
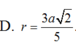
Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Bán kính r của mặt cầu ngoại tiếp hình chóp SABC bằng
![]()
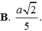
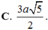
![]()
Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Tính bán kính r của mặt cầu ngoại tiếp hình chóp SABC.
A. r = a 5 2
B. r = a 2 5
C. r = 3 a 5 2
C. r = 3 a 2 5
Cho hình chóp SABC có đáy là tam giác vuông tại B, A C = 2 a . SA vuông góc với đáy, S A = a . Bán kính r của mặt cầu ngoại tiếp hình chóp SABC bằng
A. a 5 2
B. a 2 5
C. 3 a 5 2
D. 3 a 2 5