3.

\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)

Hàm nghịch biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)

\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)

4.

\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)

Hàm đồng biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)

\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Hàm số có tập xác định là R \(\Leftrightarrow x^2-2mx-2m+3\ge0\forall x\in R\)

\(\Leftrightarrow\Delta'=m^2+\left(2m-3\right)\leq0\)

\(\Leftrightarrow\left(m-1\right)\left(m+3\right)\le0\Leftrightarrow-3\le m\le1\).

Các gt nguyên âm của m thoả mãn là : -3; -2; -1.

Vậy có 3 gt nguyên âm của m thoả mãn.

+ Hàm số xác định và liên tục với mọi x> 0.

Ta có  y ' = 3 x 2 + m + 1 x 6 ,   ∀ x ∈ 0 ;   + ∞

+  Hàm số đồng biến trên khoảng (0; +∞)  khi và chỉ khi  y ' = 3 x 2 + m + 1 x 6 ≥ 0   với mọi x> 0.

⇔ m ≥ - 3 x 2 - 1 x 6 = g ( x ) ,   ∀ x ∈ ( 0 ; + ∞ ) ⇔ m ≥ m a x x ∈ ( 0 ; + ∞ ) g ( x ) . g ' ( x ) = - 6 x + 6 x 7 = - 6 x 8 + 6 x 7 = 0 ⇔ x = 1

Bảng biến thiên

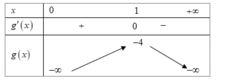
Suy ra maxg( x) = g(1) = -4 và do đó để hàm số đã cho đồng biến t với x> 0 thì m≥ -4

 Mà m nguyên âm nên m ∈ - 4 ; - 3 ; - 2 ; - 1 .

Chọn A.

Chọn đáp án A.

Tham khảo

- Với \(m=1\) thỏa mãn

- Với \(m\ne1\):

\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)

\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương

TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)

TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu

\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)

\(\Rightarrow-3< m< 1\) 

Vậy \(-3< m\le1\)

\(\Leftrightarrow\left(m+1\right)x\ge-2m-3\)

- Với \(m=-1\) thỏa mãn

- Với \(m>-1\Rightarrow x\ge\dfrac{-2m-3}{m+1}\)

\(\Rightarrow\dfrac{-2m-3}{m+1}\le-3\) \(\Leftrightarrow\dfrac{2m+3}{m+1}-3\ge0\Leftrightarrow\dfrac{-m}{m+1}\ge0\)

\(\Rightarrow-1< m\le0\Rightarrow m=0\)

- Với \(m< -1\Rightarrow x\le\dfrac{-2m-3}{m+1}\Rightarrow\dfrac{-2m-3}{m+1}\ge-1\)

\(\Rightarrow\dfrac{2m+3}{m+1}-1\le0\Leftrightarrow\dfrac{m+2}{m+1}\le0\)

\(\Rightarrow-2\le m< -1\Rightarrow m=-2\)

Vậy \(m=\left\{-2;-1;0\right\}\)

\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)

Hàm có 2 cực trị khi:

\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)

\(\Rightarrow-2m^2-4m+7>0\)

\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)

\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)

Xét hàm số y= 3x⁴- 4x³-12x²+m

Có 

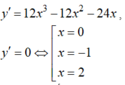
Ta có bảng biến thiên

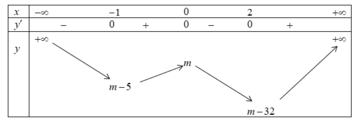
Từ bảng biến thiên, để hàm số đã cho có 7 cực trị thì  m - 5 < 0 m > 0 ⇔ 0 < m < 5 .

Vì m  nguyên nên các giá trị cần tìm của m  là m ∈ 1 ;   2 ;   3 ;   4 .

Chọn A.