Cho cos α = - 2 3 , π 2 < α < π . Khẳng định nào sau đây đúng?
A. tan α = - 5 2
B. tan α = 5 2
C. c o t α = - 5 2
D. c o t α = 5 2
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cos(α - π/2)
Vì π < α 3π/2 thì π/2 < α - π/2 < π, do đó cos(α - π/2) < 0
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Rút gọn biểu thức
\(E = cot(5π+α).cos(α-\dfrac{3π}{2})+cos(α-2π)-2.cos(\dfrac{π}{2}+α)\)\(D = sin(π+α)-cos(\dfrac{π}{2}-α)+cot(4π-α)+tan(\dfrac{5π}{2}-α)\)
Cho P = sin(π + α).cos(π - α) và Q = sin π 2 - α . cos π 2 + α .Mệnh đề nào dưới đây là đúng ?
A. P – Q = 1
B. P + Q = 2
C. P + Q = 0
D. P – Q = 0
Chọn C.
Ta có :
P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.
Và ![]() = cos α.(-sin α) = -sin α.cos α.
= cos α.(-sin α) = -sin α.cos α.
Do đó; P + Q = 0.
cho goc α thoa man π/2<α<π va sin α=1/3.tinh cos α
rut gon bieu thuc F=cosx.tan x/sin2x-cotx .cosx
Bài 1 :
Ta có : a thuộc góc phần tư thứ II .
=> Cos a < 0
- Ta lại có : \(\left\{{}\begin{matrix}sina=\dfrac{1}{3}\\sin^2a+cos^2a=1\end{matrix}\right.\)
\(\Rightarrow cosa=\sqrt{1-\left(\dfrac{1}{3}\right)^2}=-\dfrac{2\sqrt{2}}{3}\)
Bài 2 :
Ta có : \(F=\dfrac{\cos x.\tan x}{\sin^2x-\cot x.\cos x}=\dfrac{\cos x.\dfrac{\sin x}{\cos x}}{\sin^2x-\dfrac{\cos x}{\sin x}.\cos x}\)
\(=\dfrac{\sin x}{\sin^2x-\dfrac{\cos^2x}{\sin x}}=\dfrac{1}{\sin x-\cot^2x}\)
Cho 0<α<π/2. Xét dấu A=cos(α+π)
Cho π < α < 3 π 2 Khẳng định nào sau đây đúng?
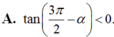
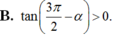
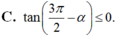
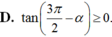
Cho π < α < 3 π 2 . Khẳng định nào sau đây đúng?
A. c o t ( 3 π 2 - α ) < 0
B. c o t ( 3 π 2 - α ) > 0
C. c o t ( 3 π 2 - α ) ≤ 0
D. c o t ( 3 π 2 - α ) ≥ 0