Tìm số đo của các góc lượng giác (OA, OE) và (OA, OP) trên hình 46 (điểm E là điểm chính giữa của cung(A'B'), sđ cung AP = 1/3 sđ cung AB). Viết số đo này theo đơn vị radian và theo đơn vị độ.
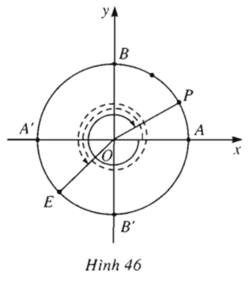
(OA, OE) = sđ cung(AE)= sđ cung(AB') + sđ cung(B'E) = - 90o + (-45)o = -135o = -3/4π (rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = π/6 rad.
Một vật dao động điều hòa với biên độ A, tần số góc ω. Chọn gốc thời gian lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là: A. x= Acos(ωt+π/4) B. x= Acos(ωt-π/2) C. x= Acos(ωt+π/2) D. x= Acos(ωt) [Cho mik lời giải chi tiết vs ạ]
Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
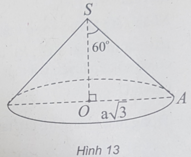
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
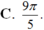
Một con lắc đơn đang dao động điều hòa với biên độ góc bằng 0,05 π rad dưới tác dụng của trọng lực. Ở thời điểm ban đầu, dây treo con lắc lệch khỏi phương thẳng đứng góc bằng 0,025 π rad và vật đang chuyển động về vị trí cân bằng theo chiều âm với tốc 75 2 π 2 cm/s Lấy g = π 2 m / s 2 Phương trình dao động của vật là
A. α = 0 , 05 πcos ( 4 πt + π 3 ) rad
B. α = 0 , 05 πcos ( πt - 2 π 3 ) rad
C. α = 0 , 05 πcos ( 2 πt + 2 π 3 ) rad
D. α = 0 , 05 πcos ( πt + π 3 ) rad
Đáp án D
Thời điểm ban đầu con lắc đang ở vị trí có li độ α = α 0 2 và đang chuyển động theo chiều âm ⇒ φ 0 = π 3
Áp dụng công thức độc lập giữa biên độ dài, li độ và vận tốc, ta có:
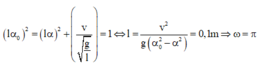
Cho hình vẽ, biết góc A=90, B=61. Tính số đo x,y?
Hãy xác định số đo góc đặc biệt theo radian.
Số đo theo độ | 00 | 300 | 450 | 600 | 900 | 1800 | 3600 |
Số đo theo radian |
|
|
|
|
|
|
|
| Số đo theo độ | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | \(180^\circ\) | \(360^\circ\) |
| Số đo theo radian | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(2\pi\) |
Hãy xác định số đo góc đặc biệt theo radian.
Số đo theo độ | 00 | 300 | 450 | 600 | 900 | 1800 | 3600 |
Số đo theo radian |
|
|
|
|
|
|
|
Số đo theo độ | 00 | 300 | 450 | 600 | 900 | 1800 | 3600 |
Số đo theo radian | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\pi \) | \({2\pi }\) |
Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.
