Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Khi đó M N → bằng:
A. 1 2 A C → + D B →
B. 1 2 A C → + B D →
C. 1 2 A D → + B C →
D. 1 2 A C → + B D →
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó tứ giác MNPQ là hình gì? Tại sao?
Xét ΔABD có : M là trung điểm AB (gt)
Q là trung điểm AD (gt)
=> MQ là đường trung bình của ΔABD
=> MQ // BD ; MQ = 1/2 BD (1)
Xét ΔCBD có : N là trung điểm BC (gt)
P là trung điểm CD (gt)
=> NP là đường trung bình của ΔCBD
=> NP // BD ; NP = 1/2 BD (2)
Từ (1) và (2) => MQ // NP; MQ = NP
Xét tứ giác MNPQ có : MQ // NP (cmt)
MQ = NP (cmt)
=> Tứ giác MNPQ là hình bình hành
Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm của AB và CD.
a, CmR M*N < hoặc = 1/2*(A*B+C*D)
b, Khi M*N = 1/2*(A*D+B*C) thì tứ giác ABCD là hình gì?
Cho xin hướng giải!!!
Bài 1: Cho tứ giác ABCD
a. Có bao nhiêu vectơ khác 0 được thiết lập từ các điểm A, B, C, D.
b. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. CMR: MQ = NP
Bài 2: Cho tứ giác ABCD. CMR: Tứ giác đó là hình bình hành khi và chỉ khi AB = DC
Giúp mình gấp với ạ :((
CÂU 11: Cho tứ giác ABCD, và AC IBD ; Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó MNPQ là hình gì? a) c/m MNPQ là hình chữ nhật
Xét ΔABC có
M là trung điểm của BA
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trungb bình
=>QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm đối xứng với M qua N. Khi đó khẳng định nào sau đây đúng?
A. M K → = A D → - B C →
B. M K → = A D → + B C →
C. M K → = A B → - C D →
D. M K → = A C → - B D →
Tứ giác DMCK có hai đường chéo cắt nhau tại trung điểm mỗi đường (N là trung điểm của MK và CD). Do đó, tứ giác DMCK là hình bình hành.
Theo quy tắc hình bình hành ta có:
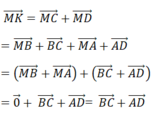
Đáp án B
Bài 1. Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của BC và AD. C/m tứ giác BMDN là hình bình hành.
Bài 2. Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Gọi P là giao điểm của DM và AN. Gọi Q là giao điểm của CM và BN. C/m tứ giác PMQN là hình bình hành.
Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Giúp mik ik hình j
Cho tam giác ABC vuông tại A, trung tuyến AM. Biết AB = 5cm, AC = 12 cm, khi đó độ dài trung tuyến AM là:
(1 Point)
6,5 cm
6 cm
5 cm
13 cm
2
Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Để tứ giác MNPQ là hình chữ nhật khi đó tứ giác ABCD cần thêm điều kiện là:
(1 Point)
AC ⊥ BD
AB = CD
AC = BD
AD = AB
3
Cho hình thang cân ABCD (AB // CD) , biết CD = 12cm, AB = 6cm, AD = 5cm. Khi đó độ dài đường cao hình thang là:
(1 Point)
3 cm
4,5 cm
4 cm
4
Trong các hình vẽ đưới đây, tứ giác là hình bình hành là:
(1 Point)
Tứ giác ABCD, tứ giác IXYZ, tứ giác MNPQ.
Tứ giác ABCD, tứ giác MNPQ, tứ giác TSQR.
Tứ giác ABCD, tứ giác MNPQ.
Cả 4 tứ giác.
5
Cho hình vẽ sau: biết góc ADE = 73 độ, góc ABC = 73 độ , D là trung điểm của AB, AE = 6cm. Khi đó độ dài AC là:
(1 Point)
6 cm
9 cm
12 cm
6
Chọn khẳng định SAI trong các khẳng định sau:
(1 Point)
Đường thẳng đi qua trung điểm 2 cạnh đáy của hình thang là trục đối xứng của hình thang.
Tam giác đều có 3 trục đối xứng
Trục đối xứng của tam giác cân là đường thẳng chứa đường trung tuyến ứng với cạnh đáy của tam giác.
Đường tròn có vô số trục đối xứng
7
Chọn khẳng định SAI trong các khẳng định sau:
(1 Point)
Hình thang có 1 góc vuông là hình chữ nhật.
Hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật.
Hình bình hành có 1 góc vuông là hình chữ nhật.
Tứ giác có 3 góc vuông là hình chữ nhật.
8
Cho hình thang ABCD (AB // CD), biết , AM và BM là các tia phân giác của các góc A và B của hình thang (M thuộc CD). Khi đó chu vi của hình thang ABCD là:
(1 Point)
24 cm
22 cm
23 cm
9
Trong các hình vẽ sau đây, tứ giác là hình thang cân là:
(1 Point)
Tứ giác ABCD, tứ giác MNQP, tứ giác RSTU
Tứ giác ABCD, tứ giác IJKL, tứ giác MNQP
Cả 4 tứ giác
Tứ giác ABCD, tứ giác MNQP
10
Trong các khẳng định sau, khẳng định nào SAI:
(1 Point)
2 điểm M và N đối xứng với nhau qua điểm O khi O là trung điểm của MN.
Hai tam giác đối xứng qua 1 điểm thì bằng nhau.
Hình bình hành có 1 tâm đối xứng.
Tâm đối xứng của tam giác đều là trọng tâm của tam giác
Submit
CÂU 10: Cho tứ giác ABCD, và AC = BD ; Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất. a) c/m MNPQ là hình thôi
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
DO đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔBAD
Suy ra: MQ=BD/2=AC/2(3)
Từ (1), (2) và (3) suy ra MNPQ là hình thoi
Xét tam giác ABD có:
M là trung điểm của AB (gt).
Q là trung điểm của DA (gt).
=> MQ là đường trung bình.
=> 2MQ = BD (Tính chất đường trung bình). (1)
Xét tam giác ABC có:
M là trung điểm của AB (gt).
N là trung điểm của BC (gt).
=> MN là đường trung bình.
=> 2MN = AC (Tính chất đường trung bình). (2)
Xét tam giác ADC có:
Q là trung điểm của DA (gt).
P là trung điểm DC (gt).
=> PQ là đường trung bình.
=> 2PQ = AC (Tính chất đường trung bình) (3)
Xét tam giác BCD có:
N là trung điểm của BC (gt).
P là trung điểm của DC (gt).
=> PN là đường trung bình.
=> 2PN = BD (Tính chất đường trung bình). (4)
Lại có: AC = BD (gt). (5)
Từ (1) (2) (3) (4) (5) => MN = NP = PQ = MQ.
=> MNPQ là hình thoi.