Khai triển đa thức 1 - 3 x 20 = a 0 + a 1 x + a 2 x 2 + . . . + a 20 x 20 . Tính tổng S = a 0 + 2 a 1 + 3 a 2 + . . . + 21 a 20
A. 4 20
B. 4 21
C. 4 22
D. 4 23
Bài 3: Cho đa thức H(x) = ( 2x – 1)20.
a) Tính tổng hệ số của đa thức H(x) khi khai triển .
b) Tính tổng hệ số bậc chẵn trừ tổng hệ số bậc lẽ của đa thức H(x) khi khai triển .
Kết quả khai triển (x - 1)^3 là đa thức :
Khai triển đa thức: \(\left(2x+1\right)\left(x+3\right)+\left(x+1\right)^2\left(x+2\right)+\left(x+5\right)\left(x+1\right)\) (có thể sử dụng máy tính casio để hỗ trợ trong việc khai triển đa thức.
\(\left(2x+1\right)\left(x+3\right)+\left(x+1\right)^2\left(x+2\right)+\left(x+5\right)\left(x+1\right)\)
\(=2x^2+6x+x+3+x^3+2x^2+x+2x^2+4x+2+x^2+x+5x+5\)
\(=x^3+7x^2+18x+10\)
đúng ko nhỉ?
tham khảo : KHAI TRIỂN RÚT GỌN ĐA THỨC BẰNG CASIO (1LINK DUY NHẤT) - YouTube
Khai triển đa thức ( 1 - 3 x ) 20 = a 1 x 1 + a 2 x 2 + . . . + a 20 x 20
Tính tổng S = a 0 + 2 a 1 + . . . + 21 a 20
A. 4 20
B. 4 21
C. 4 22
D. 4 23
khai triển các đa thức sau bằng nhị thức Newton
(x-3)^4 , (x-2y)^5 , (2x+1)^4 , (x-2)^4 , (3x-2y)^4
Tìm hệ số chứa x5 trong khai triển đa thức P(x)= (2x+1)+ (2x+1)2+ (2x+1)3+...+(2x+1)20.
mọi người ai biết giải giúp e với ạ.
ta có : \(P\left(x\right)=\sum\limits^{20}_{k=1}\left(2x+1\right)^k=\sum\limits^{20}_{k=1}C_k^p\left(2x\right)^{k-p}\left(1\right)^k\)
để có : \(x^5\Rightarrow k-p=5\)
\(\Rightarrow\) hệ số của \(P\left(x\right)\) trong khai triển là : \(\sum\limits^{20}_{k=1}C^p_k\left(2\right)^{k-p}=C^0_52^5+C^1_62^5+C^2_72^5+...+C^{15}_{20}2^5\)
\(=32\left(C^0_5+C^1_6+C^2_7+...+C^{15}_{20}\right)=32.54264=1736448\)
vậy hệ số của \(x^5\) trong khai triển đa thức \(P\left(x\right)\) là \(1736448\)
Khai triển thành đa thức
A=(x-a)^2.(x+a)^2
B=(1+a)(1-a)(1+a^2)(1+a^4)
\(A=\left(x-a\right)^2.\left(x+a\right)^2\) =\(\left[\left(x-a\right)\left(x+a\right)\right]^2\)
= \(\left(x^2-a^2\right)^2\) = \(x^4-2x^2a^2+a^4\)
\(B=\left(1+a\right)\left(1-a\right)\left(1+a^2\right)\left(1+a^4\right)\) = \(\left(1-a^2\right)\left(1+a^2\right)\left(1+a^4\right)\)
= \(\left(1-a^4\right)\left(1+a^4\right)\) = \(1-a^8\)
Tìm hệ số cuả x 8 trong khai triển đa thức f ( x ) = 1 + x 2 ( 1 - x ) 8
A: 218
B: 232
C: 238
D: tất cả sai
Lời giải.
Cách 1:
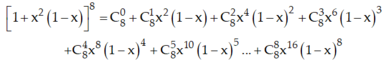
Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8.
Do đó x8 chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là:![]() .
.
Vậy hệ số cuả x8 trong khai triển đa thức 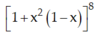 là:
là:
![]()
Cách 2: Ta có:
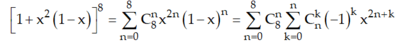
với 0 ≤ k ≤ n ≤ 8.
Số hạng chứa x8 ứng với 2n + k = 8 ⇒ k = 8 -2n là một số chẵn.
Thử trực tiếp ta được k = 0, n =4 và k = 2, n = 3.
Vậy hệ số của x8 là ![]()
Chọn C.
cho đa thức F(x)= (2017x-2018)2019
khi khai triển ta đc đa thức bậc 2019
Tính tổng các hệ số của các số hạng của đa thức sau khi khai triển
Tìm hệ số của x13 trong khai triển \(f\left(x\right)=\left(\dfrac{1}{4}+x+x^2\right)^3\left(2x+1\right)^{15}\) thành đa thức
\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....