Cho log12 3 = a . Tính log24 18 theo a
Những câu hỏi liên quan
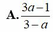
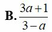
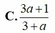
Cho log12 3 = a . Tính log24 18 theo a
Biết log275 a; log87 b; log23 c thì log12 35 tính theo a; b; c bằng: A.
3
(
b
+
a
c
)
c
+
2
B.
3
b
+
2
a
c
c
+...
Đọc tiếp
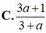
Biết log275 = a; log87 = b; log23 = c thì log12 35 tính theo a; b; c bằng:
A. 3 ( b + a c ) c + 2
B. 3 b + 2 a c c + 1
C. 3 b + 2 a c c + 2
D. 3 ( b + a c ) c + 1
Cho x, y là các số thực lớn hơn 1 thỏa mãn x2 + 9y2 6xy. Tính
M
1
+
log
12
x
+
log
12
y
2
.
log
12
...
Đọc tiếp
Cho x, y là các số thực lớn hơn 1 thỏa mãn x2 + 9y2 = 6xy. Tính M = 1 + log 12 x + log 12 y 2 . log 12 ( x + 3 y ) .
A. M = 1.
B. M = 1 + log 12 3 y log 12 6 .
C. M = 2.
D. M = log12 6.
Đáp án A.
Ta có x2 + 9y2 = 6xy <=> (x – 3y)2 = 0 <=> x = 3y.
⇒ M = 1 + log 12 x + log 12 y 2 . log 12 6 y = log 12 12 + log 12 3 y 2 log 12 36 y 2
= log 12 36 y 2 log 12 36 y 2 = 1 .
Đúng 0
Bình luận (0)
Giải bất phương trình:
\(log12(2x+3)>log12(3x+1)(1)log12(2x+3)>log12(3x+1)(1) \)
Giải bất phương trình
log
1
2
(
2
x
+
3
)
log
1
2
(
3
x
+
1
)
A.
-
1
3
x
2
B.
-
1...
Đọc tiếp
Giải bất phương trình log 1 2 ( 2 x + 3 ) > log 1 2 ( 3 x + 1 )
A. - 1 3 < x < 2
B. - 1 3 < x < 5
C. x > 5
D. x > 2
Nghiệm của bất phương trình
log
1
2
(
2
x
+
3
)
log
1
2
(
3
x
+
1
)
là
Đọc tiếp
Nghiệm của bất phương trình log 1 2 ( 2 x + 3 ) > log 1 2 ( 3 x + 1 ) là
Tìm khẳng định đúng trong các khẳng định sau:A.
4
log
2
3
4
log
3
2
B.
log
2
4...
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau:
A. 4 log 2 3 < 4 log 3 2 B. log 2 4 = log 4 2
C. log 3 3 5 > log 3 2 3 D. log 3 4 5 > log 3 4 6
log 2 4 + log 2 10 log 2 20 + 3 log 2 2
log 2 4 + log 2 10 log 2 20 + 3 log 2 2 = log 2 40 log 2 160
Đúng 0
Bình luận (0)
24 tháng 1 2022 lúc 21:55
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{ABC}.A'B'C'=AA'.S_{ABC}=2a.\dfrac{a^2\sqrt{3}}{2}=a^3\sqrt{3}\)
Chọn A
Đúng 1
Bình luận (0)
Xem thêm câu trả lời