Tìm tất cả các số thực x, y sao cho x 2 - 1 + yi = -1 + 2i
A . x = - 2 , y = 2
B . x = 2 , y = 2
C . x = 0 , y = 2
D . x = 2 , y = - 2
Những câu hỏi liên quan
Tìm tất cả giá trị thực x, y sao cho
2
x
-
3
-
y
i
y
+
4
+
x
+
2
y
-
2
i
, trong đó i là đơn vị ảo A. x 1; y -2 B. x -1; y 2 C.
x
17
7
;...
Đọc tiếp
Tìm tất cả giá trị thực x, y sao cho 2 x - 3 - y i = y + 4 + x + 2 y - 2 i , trong đó i là đơn vị ảo
A. x = 1; y = -2
B. x = -1; y = 2
C. x = 17 7 ; y = 6 7
D. x = - 17 7 ; y = - 6 7
Tìm tất cả các số thực x, y sao cho
1
−
x
2
−
y
i
i
3
−
i
2
−
i
. A.
x
2
,
y
2
B.
x
0
,
y
2
C.
x
−
2...
Đọc tiếp
Tìm tất cả các số thực x, y sao cho 1 − x 2 − y i = i 3 − i 2 − i .
A. x = 2 , y = 2
B. x = 0 , y = 2
C. x = − 2 , y = 2
D. x = 2 , y = 0
Tìm các số thực x,y thỏa mãn (3-2i)(x-yi)-4(1-i)(2+i)(x+yi) A.. B. . C. . D. .
Đọc tiếp
Tìm các số thực x,y thỏa mãn (3-2i)(x-yi)-4(1-i)=(2+i)(x+yi)
A.
.
B. 
.
C. 
.
D. 
.
Tìm các số thực x, y sao cho: 3x+yi=2y+1+(2-x)i
Tìm tất cả x, y sao cho
1
-
x
2
-
y
i
i
3
-
i
2
-
i
A.
x
2
,
y
2
B.
x
0
,
y
2
C.
x
-
2
,...
Đọc tiếp
Tìm tất cả x, y sao cho 1 - x 2 - y i = i 3 - i 2 - i
A. x = 2 , y = 2
B. x = 0 , y = 2
C. x = - 2 , y = 2
D. x = 2 , y = 0
Chọn B.
Phương pháp: Sử dụng điều kiện bằng nhau của hai số phức:” Hai số phức bằng nhau khi phần thực và phần ảo tương ứng bằng nhau”.
Cách giải: Ta có:
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 18:58
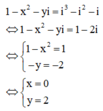
a) Tìm tất cả các số thực x sao cho x2 = 4.
b) Tìm tất cả các số thực x sao cho x3 = - 8.
a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
1
-
2
i
;
z
2
x
-
4
+
y
i
với
(
x
,
y
∈
R
)
. Tìm cặp (x;y) để
z
2
2
z
1
¯
.
Đọc tiếp
Cho hai số phức z 1 = 1 - 2 i ; z 2 = x - 4 + y i với ( x , y ∈ R ) . Tìm cặp (x;y) để z 2 = 2 z 1 ¯ .
Cho hai số phức
z
1
1
-
2
i
,
z
2
x
-
4
+
y
i
với
(
x
,
y
∈
R
)
. Tìm cặp (x,y) để
z
2
2
z
1
A. (x,y)(4;6) B. (x,y...
Đọc tiếp
Cho hai số phức z 1 = 1 - 2 i , z 2 = x - 4 + y i với ( x , y ∈ R ) . Tìm cặp (x,y) để z 2 = 2 z 1
A. (x,y)=(4;6)
B. (x,y)=(5;-4)
C. (x,y)=(6;-4)
D. (x,y)=(6;4)
Tìm tất cả các số thực x, y sao cho 1 -
x
2
-
y
.
i
i
3
-
i
2
-
i
. A. x
2
, y 2 B. x 0, y 2 C. x -
2
, y 2 D. x 2, y 0
Đọc tiếp
Tìm tất cả các số thực x, y sao cho 1 - x 2 - y . i = i 3 - i 2 - i .
A. x = 2 , y = 2
B. x = 0, y = 2
C. x = - 2 , y = 2
D. x = 2, y = 0
