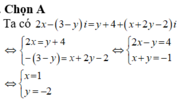Các câu hỏi tương tự
Tìm các số thực x,y thỏa mãn
x
-
2
+
y
-
3
i
1
-
2
i
với i là đơn vị ảo
Đọc tiếp
Tìm các số thực x,y thỏa mãn x - 2 + y - 3 i = 1 - 2 i với i là đơn vị ảo
![]()
![]()
![]()
![]()
Tìm các số thực x,y thỏa mãn (x+y) + (x-y)i = 3+5i với i là đơn vị ảo.
![]()
![]()
![]()
![]()
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
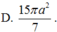
Cho i là đơn vị ảo. Với
x
,
y
∈
ℝ
thì x-1+(y+3)i là số thuần ảo khi và chỉ khi
Đọc tiếp
Cho i là đơn vị ảo. Với x , y ∈ ℝ thì x-1+(y+3)i là số thuần ảo khi và chỉ khi
![]()
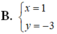
![]()
Cho hai số thực x, y thỏa mãn
2
x
+
1
+
(
1
-
2
y
)
i
2
(
2
-
i
)
+
y
i
-
x
khi đó giá trị của
x
2
-
...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 2 x + 1 + ( 1 - 2 y ) i = 2 ( 2 - i ) + y i - x khi đó giá trị của x 2 - 3 x y - y bằng:
A. -1.
B. 1.
C. -2.
D. -3.
Cho hai số thực x,y thỏa mãn điều kiện:`x^4+y^4+6x^2y^2+2=2x^2+3y^2`
Tính giá trị lớn nhất và nhỏ nhất của `P=(-6x^2-5y^2-4x^2y^2-7)/(x^2+y^2+1)`
Thầy Lâm cứu em :<<
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 7 : Tìm tập hợp tất cả các giá trị của m để hàm số \(y=x^3+\left(3m-1\right)x^2+m^2x-3\) đạt cực tiểu tại x=-1