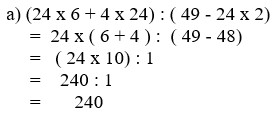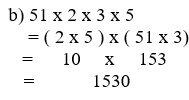4. ( x + 2 ) = 24

Những câu hỏi liên quan
Tính nhanh
a) (24 x 6 + 4 x 24) : ( 49 - 24 x 2)
b) 51 x 2 x 3 x 5
1) 54 : x - x : x = 3 x 2 - 1
2) 42 : x + x - x = 4 x 3 - 4
3) 24 : x - 2 x 4 = 24 - 2 x 3 x 4
1, 54 : x - 1 = 5
54 : x = 5+1 = 6
x = 54 : 6 = 9
2, 42 : x + 0 = 8
x = 42 : 8 = 21/4
3, 24 : x - 8 = 0
24 : x = 0 + 8 = 8
x = 24 : 8 = 3
Tk mk nha
Đúng 0
Bình luận (0)
1) 54:x-x:x=3x2-1
54:x- 1 =6-1
54:x- 1=5
54:x =6
x=54:6=9
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải pt
a 4(x+3)^2=(2x+6)^2
b (3x+4)^2=4(x+3)
c (6x+3)^2=(x-4)^2
d (x^2+3x+2)(x^2+3x+3)-2=0
e(x^2-5x)+10(x^2-5x)+24=0
f(x^2+x+1)(x^2+x+2)=12
gx(x+1)(x-1)(x+2)=24
h(x+1)(x+2)(x+3)(x+4)-24=0
lm giúp mik nha các bn
a) \(4\left(x+3\right)^2=\left(2x+6\right)^2\)
\(\Leftrightarrow2^2\left(x+3\right)^2=\left(2x+6\right)^2\)
\(\Leftrightarrow\left(2x+6\right)^2=\left(2x+6\right)^2\)
Vậy tập nghiệm của phương trình là \(S=ℝ\)
b) \(\left(3x+4\right)^2=4\left(x+3\right)\)
\(\Leftrightarrow9x^2+24x+16=4x+12\)
\(\Leftrightarrow9x^2+20x+4=0\)
\(\Leftrightarrow\left(9x+2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}9x+2=0\\x+2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{2}{9}\\x=-2\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{-\frac{2}{9};-2\right\}\)
c) \(\left(6x+3\right)^2=\left(x-4\right)^2\)
\(\Leftrightarrow\orbr{\begin{cases}6x+3=x-4\\6x+3=4-x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}5x+7=0\\7x-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{7}{5}\\x=\frac{1}{7}\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{-\frac{7}{5};\frac{1}{7}\right\}\)
d) \(\left(x^2+3x+2\right)\left(x^2+3x+3\right)-2=0\)
Đặt \(t=x^2+3x+2\), ta có :
\(t\left(t+1\right)-2=0\)
\(\Leftrightarrow t^2+t-2=0\)
\(\Leftrightarrow\left(t+2\right)\left(t-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+2=0\\t-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+3x+4=0\\x^2+3x+1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+\frac{3}{2}\right)^2+\frac{7}{4}=0\left(ktm\right)\\\left(x+\frac{3}{2}\right)^2-1,25=0\left(tm\right)\end{cases}}\)
\(\Leftrightarrow x=\pm\sqrt{1,25}-\frac{3}{2}=-\frac{3\pm\sqrt{5}}{2}\)(tm)
Vậy tập nghiệm của phương trình là \(S=\left\{-\frac{3\pm\sqrt{5}}{2}\right\}\)
e)Đề bài sai ! Mik sửa :
\(\left(x^2-5x\right)^2+10\left(x^2-5x\right)+24=0\)
Đặt \(t=x^2-5x\), ta có :
\(t^2+10t-24=0\)
\(\Leftrightarrow\left(t+12\right)\left(t-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+12=0\\t-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-5x+12=0\\x^2-5x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-\frac{5}{2}\right)^2+\frac{23}{4}=0\left(ktm\right)\\\left(x-\frac{5}{2}\right)^2-\frac{33}{4}=0\left(tm\right)\end{cases}}\)
\(\Leftrightarrow x=\pm\frac{\sqrt{33}}{2}+\frac{5}{2}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{\sqrt{33}}{2}+\frac{5}{2};-\frac{\sqrt{33}}{2}+\frac{5}{2}\right\}\)
f) \(\left(x^2+x+1\right)\left(x^2+x+2\right)=12\)
\(\Leftrightarrow\left(x^2+x+1\right)\left(x^2+x+2\right)-12=0\)
Đặt \(t=x^2+x+1\), ta có :
\(t\left(t+1\right)-12=0\)
\(\Leftrightarrow t^2+t-12=0\)
\(\Leftrightarrow\left(t+4\right)\left(t-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+4=0\\t-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+x+5=0\\x^2+x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+\frac{1}{2}\right)^2+\frac{19}{4}=0\left(ktm\right)\\\left(x+\frac{1}{2}\right)^2-\frac{9}{4}=0\left(tm\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}-\frac{1}{2}=1\left(tm\right)\\x=-\frac{3}{2}-\frac{1}{2}=-2\left(tm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{1;-2\right\}\)
g) \(x\left(x+1\right)\left(x-1\right)\left(x+2\right)=24\)
\(\Leftrightarrow\left(x^2+x\right)\left(x^2+x-2\right)-24=0\)
Đặt \(t=x^2+x\), ta có :
\(t\left(t-2\right)-24=0\)
\(\Leftrightarrow t^2-2t-24=0\)
\(\Leftrightarrow\left(t+4\right)\left(t-6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+4=0\\t-6=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+x+4=0\\x^2+x-6=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+\frac{1}{2}\right)^2+\frac{15}{4}=0\left(ktm\right)\\\left(x+\frac{1}{2}\right)^2-\frac{25}{4}=0\left(tm\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{2}-\frac{1}{2}=2\left(tm\right)\\x=-\frac{5}{2}-\frac{1}{2}=-3\left(tm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{2;-3\right\}\)
h) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24=0\)
\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)
Đặt \(t=x^2+5x+4\), ta có :
\(t\left(t+2\right)-24=0\)
\(\Leftrightarrow t^2+2t-24=0\)
\(\Leftrightarrow\left(t+6\right)\left(t-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+6=0\\t-4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+5x+10=0\\x^2+5x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+\frac{5}{2}\right)^2+\frac{15}{4}=0\left(ktm\right)\\x\left(x+5\right)=0\left(tm\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\left(tm\right)\\x=-5\left(tm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{0;-5\right\}\)
Tính nhẩm
5 x 6 = ..... 2 x 6 = ..... 3 x 6 = ..... 4 x 6 = .....
6 x 5 = ..... 6 x 2 = ..... 6 x 3 = ..... 6 x 4 = .....
30 : 6 = ..... 12 : 6 = ..... 18 : 6 = ..... 24 : 6 = .....
30 : 5 = ..... 12 : 2 = ..... 18 : 3 = ..... 24 : 4 = .....
5 x 6 = 30 2 x 6 = 12 3 x 6 = 18 4 x 6 = 24
6 x 5 = 30 6 x 2 = 12 6 x 3 = 18 6 x 4 = 24
Đúng 0
Bình luận (0)
Tính nhẩm:
5 x 6 = 30 2 x 6 = 12 3 x 6 = 18 4 x 6 = 24
6 x 5 = 30 6 x 2 = 12 6 x 3 = 18 6 x 4 = 24
30 : 6 = 5 12 : 6 = 2 18 : 6 = 3 24 : 6 = 4
30 : 5 = 6 12 : 2 = 6 18 : 3 = 6 24 : 4 = 6
Học tốt <3
5 x 6 = 30 2 x 6 = 12 3 x 6 = 18 4 x 6 = 24
6 x 6 = 30 6 x 2 = 12 6 x 3 = 18 6 x 4 = 24
30 : 6 = 5 12 : 6 = 2 18 : 6 = 3 24 : 6 = 4
30 : 5 = 6 12 : 2 = 6 18 : 3 = 6 24 : 4 = 6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
(x2 + x + 2x + 2)(x2 + 3x + 4x + 12)24[x(x+1)+2(x+1)] [x(x+3) + x(x+3)]24(x+1)(x+2)(x+3)(x+4)24(x2 + 5x + 4)(x2 + 5x + 6) 24 {x+1 nhân x+4 và x+3 nhân x+4}Đặt x2 + 5x + 4ata đượca(a+2)24 a2 + 2a - 240 (a+1)2 - 250 (a+1)225 a+1 5 a 4 hoặc a-6thay a x2 + 5x + 4Ta có PT(1)x2+ 5x + 44 x(x+5)0 x 0 hoặc x-5PT(2)x2 + 5x + 4-6 còn lại bạn tự giải nhé!!!
Đọc tiếp
(x2 + x + 2x + 2)(x2 + 3x + 4x + 12)=24
<=>[x(x+1)+2(x+1)] [x(x+3) + x(x+3)]=24
<=>(x+1)(x+2)(x+3)(x+4)=24
<=>(x2 + 5x + 4)(x2 + 5x + 6)= 24 {x+1 nhân x+4 và x+3 nhân x+4}
Đặt x2 + 5x + 4=a
ta được
a(a+2)=24
<=> a2 + 2a - 24=0
<=> (a+1)2 - 25=0
<=> (a+1)2=25
<=> a+1 = 5
<=> a= 4 hoặc a=-6
thay a= x2 + 5x + 4
Ta có PT(1)
x2+ 5x + 4=4
<=> x(x+5)=0
<=> x= 0 hoặc x=-5
PT(2)
x2 + 5x + 4=-6
<=> còn lại bạn tự giải nhé!!!

439 x 78 - 38 x 78 - 78 24 x 13 + 6 x89 x 4 - 2 x 24
Lời giải:
a.
$23+23\times 45+23\times 44=23\times (1+45+44)=23\times 90$
$=23\times (100-10)=23\times 100-23\times 10=2300-230=2070$
b.
$=36\times 280-36\times 79-36$
$=36\times (280-79-1)=36\times (280-80)=36\times 200=7200$
c.
$=72\times 10+72\times 25+72\times 66-72$
$=72\times (10+25+66-1)=72\times 100=7200$
Đúng 0
Bình luận (0)
Tính nhanh:
3 - [2/4 x 1/2 + 2/4 x 3/2 + 24/8 x 2/4 + 2/4]
3 - [ \(\dfrac{2}{4}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) \(\times\) \(\dfrac{3}{2}\) + \(\dfrac{24}{8}\) \(\times\)\(\dfrac{2}{4}\) + \(\dfrac{2}{4}\)]
= 3 - \(\dfrac{2}{4}\) \(\times\) ( \(\dfrac{1}{2}\) + \(\dfrac{3}{2}\) + 3 + 1)
= 3 - \(\dfrac{2}{4}\) \(\times\) ( 2 + 3 + 1)
= 3 - \(\dfrac{1}{2}\) \(\times\) 6
= 3 - 3
= 0
Đúng 1
Bình luận (0)
tính bằng cách thuận tiện: 4/9 x 19/24 + 19/24 x 7/9 -19/24 x 2/9?
giúp mình với?
\(=\dfrac{19}{24}\times\left(\dfrac{4}{9}+\dfrac{7}{9}-\dfrac{2}{9}\right)=\dfrac{19}{24}\times1=\dfrac{19}{24}\)
Đúng 1
Bình luận (0)
\(\dfrac{19}{24}\times\left(\dfrac{4}{9}+\dfrac{7}{9}-\dfrac{2}{9}\right)\)
\(=\dfrac{19}{24}\times1=\dfrac{19}{24}\)
Đúng 3
Bình luận (0)
Tim so nguyen x, biet :
a/ -24 + (x + 4)^4 = 10^3
b/ 2.(x + 7) - 3.(6 - x) = -24
c/ 3x - 6x^2 = 0
a/
\(-24+\left(x+4\right)^4=10^3\)3
\(\Leftrightarrow-24+x^4+16x^3+96x^2+256x+256=10^3\)
<=>\(x^4+16x^3+96x^2+256x-768=0\)
Giải trên tập số phức ta được
\(x=-\sqrt{32}-4\)
\(x=\sqrt{32}-4\)
\(x=-\sqrt{32}i-4\)
\(x=\sqrt{32}1-4\)=> Phần a kog có giá trị nguyên nào của x thỏa mãn phương trình
b/
2(x+7)-3(6-x)=-24
<=> 2x+14-18+3x=-24
<=>5x=-20
<=>x=-4
Vậy x=-4
c/
\(3x-6x^2=0\)
\(\Leftrightarrow3x\left(1-2x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x=0\\1-2x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{2}\end{cases}}\)(x = 1/2 kog thỏa mãn yêu cầu)
Vậy x=0
Đúng 0
Bình luận (0)
a/\(\left(x+4\right)^4=1000+24\)
\(\Rightarrow x^4+8x^2+4^4-1024=0\)
\(\Rightarrow x^4+8x^2-768\)
\(\Rightarrow x^4-24x+32x-768=0\)
\(\Rightarrow x.\left(x-24\right)+32.\left(x-24\right)\)
\(\Rightarrow\left(x+32\right).\left(x-24\right)\Rightarrow\orbr{\begin{cases}x=-32\\x=24\end{cases}}\)
b/2x+14-18+3x=-24
5x=-24-14+18
x=-20/5=-4
c/3x-6x\(^2\) =0
\(3x.\left(1-2x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=0\rightarrow x=0\\1-2x=0\rightarrow x=\frac{1}{2}\end{cases}}\)
KL bAN tu lam nhe
Đúng 0
Bình luận (0)
ban HA sai hang đang thưc rôi \(\left[\left(x+4\right)^2\right]^2\) khai triên ra nhu binh thuong
Đúng 0
Bình luận (0)
giai PT a,x^4 - 5x^2 +4 = 0
b,(x^2 +5x)^2 - 2(x^2 +5x) = 24
c,(x^2 - x)^2 - 2 = x^2 -x
d, x(x+1) (x-1) (x-2) = 24
a) x4 - 5x2 + 4 = 0 (*)
đặt x2 = m (\(m\ge0\))
(*) <=> m2 - 5m + 4 = 0
m2 - 4m - m + 4 = 0
m(m - 4) - (m - 4) = 0
(m - 4)(m - 1) = 0
vậy m - 4 = 0 hoặc m - 1 = 0
hay m = 4 hoặc m = 1
m = 4 => x2 = 4 => \(x=\pm2\)
m = 1 => x2 = 1 => \(x=\pm1\)
d) \(x\left(x+1\right)\left(x-1\right)\left(x-2\right)=24\)
\(\Leftrightarrow\left[x\left(x-1\right)\right]\left[\left(x+1\right)\left(x-2\right)\right]=24\)
\(\Leftrightarrow\left(x^2-x\right)\left(x^2-x-2\right)-24=0\)
\(\Leftrightarrow\left(x^2-x\right)^2-2\left(x^2-x\right)+1-25=0\)
\(\Leftrightarrow\left(x^2-x+1\right)^2-25=0\)
\(\Leftrightarrow\left(x^2-x+6\right)\left(x^2-x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-x+6=0\left(1\right)\\x^2-x-4=0\left(2\right)\end{cases}}\)
+) Pt (1) \(\Leftrightarrow\left(x-\frac{1}{2}\right)^2=-\frac{23}{4}\) ( vô nghiệm )
+) Pt (2) \(\Leftrightarrow\left(x-\frac{1}{2}\right)^2=\frac{17}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\sqrt{17}}{4}+\frac{1}{2}\\x=-\frac{\sqrt{17}}{4}+\frac{1}{2}\end{cases}}\) ( thỏa mãn )
Vậy pt đã cho có nghiệm \(S=\left\{\pm\frac{\sqrt{17}}{4}+\frac{1}{2}\right\}\)