Tất cả các giá trị x thỏa mãn bất phương trình log 2 3 x + 1 > 3 là:
A. x > 7 3
B. - 1 3 < x < 7
C. x > - 1 3
D. x > 8 3
Tất cả các giá trị x thỏa mãn bất phương trình log 3 x - 1 > 2 là
A. x > 10
B. x < 10
C. 0 < x < 10
D. x ≥ 10
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Ta có bất phương trình thứ nhất:
\(2x+1< x+3\)
\(\Leftrightarrow2x-x< 3-1\)
\(\Leftrightarrow x\cdot\left(2-1\right)< 2\)
\(\Leftrightarrow x< 2\) (1)
Bất phương trình thứ hai:
\(5x\ge x-16\)
\(\Leftrightarrow5x-x\ge-16\)
\(\Leftrightarrow4x\ge-16\)
\(\Leftrightarrow x\ge-4\) (2)
Từ (1) và (2) ta có:
\(-4\le x< 2\)
2x+1<x+3 và 5x>=x-16
=>2x-x<3-1 và 5x-x>=-16
=>x<2 và x>=-4
=>-4<=x<2
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2
Cho biểu thức f(x) = (x + 5)(3 - x). Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là
A. x ∈ (- ∞ ;5) ∪ (3;+ ∞ )
B. x ∈ (3;+ ∞ )
C. x ∈ (-5;3)
D. x ∈ (- ∞ ;-5] ∪ [3;+ ∞ )
Chọn D.
Để f(x) ≤ 0 thì (x + 5)(3 - x) < 0
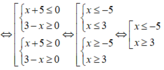
Vậy x ∈ (- ∞ ;-5] ∪ [3;+ ∞ ).
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 ≥ ( 2 ) 2
A. 4
B. 5
C. 2
D. 3
Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình 12 x + ( 2 - m ) 6 x + 3 x > 0 thỏa mãn với mọi x dương.
![]()
![]()
![]()
![]()
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình log x ( 5 x 2 - 8 x + 3 ) > 2 đều là nghiệm của bất phương trình x 2 - 2 x - a 4 + 1 ≥ 0 . Khi đó:
A. S = - 10 5 ; 10 5 .
B. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞
C. S = - 10 5 ; 10 5 .
D. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞ .
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 > 2 2 x
A. 4
B. 5
C. 2
D. 3
Ta có:
8 x . 2 1 - x 2 > 2 2 x ⇔ 2 3 x + 1 - x 2 > 2 x ⇔ 3 x + 1 - x 2 > x ⇔ x 2 - 2 x - 1 < 0 ⇔ 1 - 2 < x < 1 + 2
Mà x ∈ ℝ ⇒ x ∈ 1 ; 2 . Bất phương trình đã cho có 2 nghiệm nguyên dương.
Chọn đáp án C.