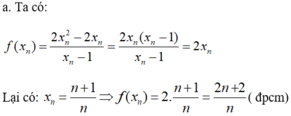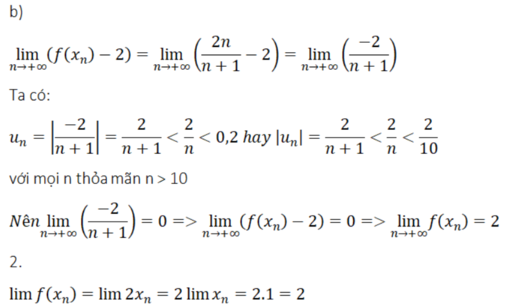Chứng minh rằng hàm số y = sinx không có giới hạn khi x → +∞

Những câu hỏi liên quan
Chứng minh rằng hàm số y = cos x không có giới hạn khi x → + ∞ .
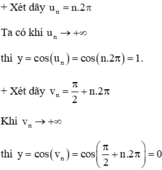
Vậy với hai dãy un và vn cùng → +∞ thì f(un) và f(vn) tiến đến hai giá trị khác nhau nên không tồn tại giới hạn của hàm số y = cos x khi x → +∞.
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số f(x) = cos(1/x) không có giới hạn khi x → 0
Chọn hai dãy số có số hạng tổng quát là 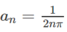 và
và 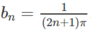 .
.
Tính và so sánh lim f ( a n ) và lim f ( b n ) để kết luận về giới hạn của f(x) khi x → 0
Đúng 0
Bình luận (0)
a) Chứng minh rằng hàm số \(y=\sin x\) không có giới hạn khi \(x\rightarrow+\infty\)
b) Giải thích bằng đồ thị kết luận ở câu a)
Chứng minh rằng hàm số \(f\left(x\right)=\cos\dfrac{1}{x}\) không có giới hạn khi \(x\rightarrow0\) ?
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y cosx, y sinx , đường thẳng
x
π
2
;
x
3
π
2
. A.
3
B.
2
2
C.
2
D. 1.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = cosx, y = sinx , đường thẳng x = π 2 ; x = 3 π 2 .
A. 3
B. 2 2
C. 2
D. 1.
Chọn B.
Đặt f1(x) = cosx, f2(x) =sinx ;
Ta có f1(x) - f2(x) = 0 <=> cosx - sinx = 0 <=> x = 5 π 4 ∈ π 2 ; 3 π 2
Diện tích hình phẳng đã cho là:

Đúng 0
Bình luận (0)
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
(
x
)
sinx
cosx
,
đường thẳng
y
0
,
x
0...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ) = sinx cosx , đường thẳng y = 0 , x = 0 và x = π 2 .
A. 1 2
B. 1
C. 1 4
D. π 2
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ
- Hàm số \(y=sin\left(x\right)\)
Tập xác định D = R.
Với mọi \(x\in R\) thì \(-x\in R\) và \(sin\left(-x\right)=-sin\left(x\right)\)
Vậy nên \(y=sin\left(x\right)\) là hàm số lẻ.
- Hàm số \(y=cot\left(x\right)\)
Tập xác định \(D=R\backslash\left\{k\pi,k\in R\right\}\)
Với mọi \(x\in R\) thì \(-x\in R\) và \(cot\left(-x\right)=-cot\left(x\right)\)
Vậy nên \(y=cot\left(x\right)\) là hàm số lẻ.
Đúng 1
Bình luận (0)
Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số
y
sin
x
,
y
cos
x
và hai đường thẳng
x
0
,
x
π
2
? A.
S
2
2
B.
S
2
1
−
2
C. ...
Đọc tiếp
Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = sin x , y = cos x và hai đường thẳng x = 0 , x = π 2 ?
A. S = 2 2
B. S = 2 1 − 2
C. S = 2 2 − 1
D. S = 2 2 − 1
Đáp án C
∫ 0 π 2 sin x − cos x d x = − ∫ 0 π 4 sin x − cos x d x + ∫ π 4 π 2 sin x − cos x d x = − 2 ∫ 0 π 4 sin x − π 4 d x + ∫ π 4 π 2 sin x − π 4 d x S = 2 . cos x − π 4 π 4 0 − 2 . cos x − π 4 π 2 π 4 = 2 1 − 1 2 − 2 1 2 − 1 = 2 2 − 2 = 2 2 − 1
“Dùng CASIO tính tích phân trị tuyệt đối, dò đáp án
Đúng 0
Bình luận (0)