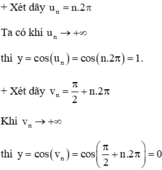
Vậy với hai dãy un và vn cùng → +∞ thì f(un) và f(vn) tiến đến hai giá trị khác nhau nên không tồn tại giới hạn của hàm số y = cos x khi x → +∞.
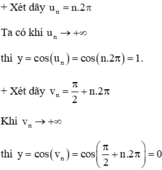
Vậy với hai dãy un và vn cùng → +∞ thì f(un) và f(vn) tiến đến hai giá trị khác nhau nên không tồn tại giới hạn của hàm số y = cos x khi x → +∞.
Chứng minh rằng hàm số f(x) = cos(1/x) không có giới hạn khi x → 0
Chứng minh rằng hàm số y = sinx không có giới hạn khi x → +∞
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
Cho hàm số f x = x 2 n ế u x ≥ 0 x 2 - 1 n ế u x < 0
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
b) Dùng định nghĩa chứng minh định nghĩa trên
Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc x: y = sin 6 x + cos 6 x + 3 . sin 2 x . cos 2 x
Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc x:
y = cos 2 π 3 - x + cos 2 π 3 + x + cos 2 2 π 3 - x + cos 2 2 π 3 + x - 2 sin 2 x
Trong biểu thức (1) xác định hàm số y = f ( x ) ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi x → 1?
Giới hạn bên phải của hàm số y = 3 x - 7 x - 2 khi x → 2 là:
A. + ∞
B. - ∞
C. 3
D. 7 2