Tham khảo

(a + b)⁴ = (a + b)³(a + b)

= (a³ + 3a²b + 3ab² + b³ )(a + b)

= a⁴ + 3a³b + 3a²b² + ab³ + a³b + 3a²b² + 3ab³ + b⁴

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Sử dụng nhị thức Niuton với a = x, b = - m2

x − m 2 4 =    x + ( − m 2 ) 4 =    C 4 0 . x 4 + ​​ C 4 1 . x 3 . − m 2 + C 4 2 . x 2 . − m 2 2 + C 4 3 . x . − m 2 3 + ​​ C 4 4 . − m 2 4 = x 4 − 4 x m 2 3 + ​    6 x 2 m 4 −    4 x . m 6 + m 8

Chọn đáp án D

Nhận xét: học sinh có thể nhầm khi áp dụng sai công thức để dẫn đến các kết quả A,B và C

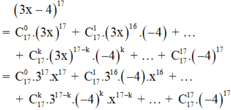
Đặt S là tổng các hệ số của đa thức khai triển.

Ta có:

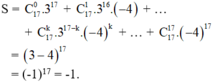
Vậy tổng các hệ số của đa thức khai triển bằng -1.

Đáp án A

Tổng các hệ số bậc chẵn khi khai triển đa thức 2 x − 1 2018 được tính bằng

S = C 2018 0 .2 2018 + C 2018 2 .2 2016 + C 2018 4 .2 2014 + ... + C 2018 2018 .2 0

Ta có   x + 1 2018 = ∑ k = 0 2018 C 2018 k x 2018 − k ; − x + 1 2018 = ∑ k = 0 2018 C 2018 k − x 2018 − k

Cộng hai vế đẳng thức trên ta được

x + 1 2018 + − x + 1 2018 = 2 ( C 2018 0 x 2018 + C 2018 2 x 2016 + C 2018 4 x 2014 + ... + C 2018 2018 x 0 )

Với x = 2  ta có   3 2018 + 1 = 2. S ⇒ S = 3 2018 + 1 2

Tổng các hệ số của đa thức f(x) = (3x – 4)¹⁷ bằng:

f(1) = (3 – 4)¹⁷= (– 1)¹⁷ = -1

a. (x + y)² = x² + 2xy + y²

b. (x - 2y)² = x² - 4xy - 4x²

c. (xy² + 1)(xy² - 1) = x²y⁴ - 1

d. (x + y)²(x - y)² = (x² + 2xy + y²)(x² - 2xy + y²) = x⁴ - (2xy + y²)² = x⁴ - (4x²y² + y⁴) = x⁴ - 4x²y² - y⁴

^{Chucs hocj toots}

Câu 2: 

a: \(x^2-4x+4=\left(x-2\right)^2\)

b: \(x^2+10x+25=\left(x+5\right)^2\)

d: \(9\left(x+1\right)^2-6\left(x+1\right)+1=\left(3x+2\right)^2\)

e: \(\left(x-2y\right)^2-8\left(x-2xy\right)+16x^2=\left(x-2y+4x\right)^2=\left(5x-2y\right)^2\)

Câu 7:

a: Ta có: \(A=x^2-2x+7\)

\(=x^2-2x+1+6\)

\(=\left(x-1\right)^2+6\ge6\forall x\)

Dấu '=' xảy ra khi x=1

b: Ta có: \(B=5x^2-20x\)

\(=5\left(x^2-4x+4-4\right)\)

\(=5\left(x-2\right)^2-20\ge-20\forall x\)

Dấu '=' xảy ra khi x=2

Ta có:(a²+ab+b²)(a²-ab+b²)-(a⁴+b⁴)

    =   (a²+b²)²-a²b²-a⁴-b⁴=a⁴+2a²b²+b⁴-a²b²-a⁴-b⁴=a²b²

Ta có:(a²+ab+b²)(a²-ab+b²)-(a⁴+b⁴)

    =   (a²+b²)²-a²b²-a⁴-b⁴=a⁴+2a²b²+b⁴-a²b²-a⁴-b⁴=a²b²