Tứ giác ABCD có AB = BC, CD = DA. Chứng minh rằng BD là đường trung trực của AC.
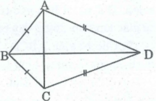
Tứ giác ABCD có AB=BC,CD=DA. Chứng minh rằng BD là đường trung trực của AC
Ta có : AB=BC
=> B thuộc đường trung trực của AC (1)
Ta có : AD=DC
=>D thuộc đường trung trực của AC (2)
(1)(2)=> BD là đường trung trực của AC
Ta có: AB=AD(GT)
SUY RA: A thuộc trung trực của BD(1) tính chất đg trung trực
CB=CD(GT)
SUY RA: C thuộc trung trực của BD(2)
từ (1)(2) suy ra AC là trung trực của BD
chắc 100%
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
Trong tam giác ABD có: MQ là đường trung bình
=> MQ = 1/2 BD (1)
Trong tam giác ABC có : MN là đường trung bình
=> MN = 1/2 AC (2)
mà AC = BD và AC vuông góc với BD (3)
Từ (1) (2) và (3) => MQ = MN và MQ vuông góc với MN
=> tứ giác MNPQ là hình vuông
Cho tứ giác ABCD có 2 đường chéo AC và BD vuông góc tại O
a. Chứng minh\(AB^{2} + CD^{2} = BC^{2} + AD^{2}
\)
b. Lấy các điểm M, N, P, Q thứ tự là trung điểm của AB, AC, CD, DA. Chứng Minh OM+ON+OQ=\(\dfrac{1}{2}\) (AB+BC+CD+DA)
a) \(AB^2+CD^2=OA^2+OB^2+OC^2+OD^2=\left(OA^2+OD^2\right)+\left(OB^2+OC^2\right)=AD^2+BC^2\)b) -Áp dụng định lí:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1 nửa cạnh huyền.
\(OM+ON+OP+OQ=\dfrac{1}{2}AB+\dfrac{1}{2}BC+\dfrac{1}{2}CD+\dfrac{1}{2}DA=\dfrac{1}{2}\left(AB+BC+CD+DA\right)\)
Cho tứ giác ABCD có AB = BC; CD = DA.
a) Chứng minh: BD là đường trung trực của AC;
b) Cho B = 100 o , D = 80o . Tính A và C
a: Ta có: BA=BC
nên B nằm trên đường trung trực của AC\(\left(1\right)\)
Ta có: CD=DA
nên D nằm trên đường trung trực của AC\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BD là đường trung trực của AC
b: Xét ΔABD và ΔCBD có
BA=BC
DB chung
DA=DC
Do đó: ΔABD=ΔCBD
Suy ra: \(\widehat{BAD}=\widehat{BCD}=\dfrac{180^0}{2}=90^0\)
65. Tứ giác ABCD có AB=BC, CD=DA (hình cái diều). Chứng minh rằng điểm A đối xứng điểm C qua đường thẳng BD
66. Tam giác ABC có AB<AC. Gọi d là đường trung trực của BC. Vẽ điểm K đối xứng với điểm A qua đường thẳng d.
a) Tìm các đoạn thẳng đối xứng với đoạn AB qua d, đối xứng với đoạn thẳng AC qua d
b) Tứ giác AKCB là hình gì ? Tại sao ?
Cho tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại O. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh tứ giác MNPQ có các cạnh bằng nhau.
b) MP cắt AC và BD tại E và F. Chứng minh rằng tam giác OEF cân
a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MN//QP và MN=QP
Xét tứ giác MNPQ có
MN//QP(cmt)
MN=QP(cmt)
Do đó: MNPQ là hình bình hành
Xét ΔABD có
Q là trung điểm của AD
M là trung điểm của AB
Do đó: QM là đường trung bình của ΔABD
Suy ra: QM//DB và \(QM=\dfrac{DB}{2}\)
hay \(QM=\dfrac{AC}{2}\)(3)
Từ (2) và (3) suy ra QM=QP
Hình bình hành MNPQ có QM=QP(cmt)
nên MNPQ là hình thoi
Cho tứ giác ABCD có AB = AD, BC = CD
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Biết góc BDA= 110°, góc BCD= 50°. Tính góc ABC, góc ADC.
c) Gọi I là giao điểm của AC và BD, chứng minh ∆ABI = ∆ADI