Tứ giác ABCD có AB = BC, CD = DA. Cho biết B = 100 0 , D = 70 0 , tính góc A và góc C.
Những câu hỏi liên quan
Tứ giác ABCD có
A
B
B
C
,
C
D
D
A
,
B
^
100
°
,
D
^
70
°
. Tính
A
^
,
C
^
.
A.
A...
Đọc tiếp
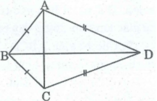
Tứ giác ABCD có A B = B C , C D = D A , B ^ = 100 ° , D ^ = 70 ° . Tính A ^ , C ^ .
A. A ^ = C ^ = 95 °
B. A ^ = 95 ° ; C ^ = 55 °
C. A ^ = C ^ = 85 °
D. Đáp án khác
Đáp án cần chọn là: A
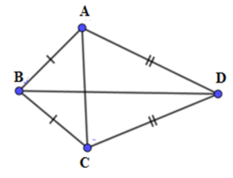
Xét tam giác ABC có: B ^ = 100 ° ; A B = B C
⇒ ∆ A B C cân tại B .
B A C ^ = B C A ^ = 180 0 − 100 0 2 = 40 0
Xét tam giác ADC có C D = D A ⇒ ∆ A D C cân tại D có A D C ^ = 70 ° nên D A C ^ = D C A ^ = 180 0 − 70 0 2 = 55 0
Từ đó ta có A ^ = B A D ^ = B A C ^ + C A D ^ = 40 ° + 55 ° = 95 °
Và C ^ = B C D ^ = B C A ^ + A C D ^ = 40 ° + 55 ° = 75 °
Nên A ^ = C ^ = 95 °
Đúng 0
Bình luận (0)
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D 1 : 2 : 3 : 4a) Tính các góc của tứ giác ABCDb) Chứng minh: AB // CDc) Gọi giao điểm của AD cắt BC E. Tính các góc của tam giác CDE Bài 2: Cho tứ giác ABCD có góc C 80^0 , D 70^0 . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIBBài 3: Cho tứ giác ABCD có AB BC; CD DAa) Chứng minh rằng BD là đường trung trực của ACb) Cho biết góc B 100^0 ; D 70^0 . Tính góc A và C
Đọc tiếp
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D = 1 : 2 : 3 : 4
a) Tính các góc của tứ giác ABCD
b) Chứng minh: AB // CD
c) Gọi giao điểm của AD cắt BC = E. Tính các góc của tam giác CDE
Bài 2: Cho tứ giác ABCD có góc C = \(80^0\) , D = \(70^0\) . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIB
Bài 3: Cho tứ giác ABCD có AB = BC; CD = DA
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho biết góc B = \(100^0\) ; D = \(70^0\) . Tính góc A và C
Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
Đúng 1
Bình luận (1)
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>
Đúng 2
Bình luận (0)
Tứ giác ABCD có AB = BC; CD = DA
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho biết \(\widehat{B}=100^0,\widehat{D}=70^0\). Tính \(\widehat{A}\) và \(\widehat{C}\) ?
cho tứ giác ABCD có AB=BC, CD=DA. a/ cm BD là đường trung t rực của AC. b/ Cho biết góc B=100 độ, góc D=70 đọ tính góc A, góc C
1) Tứ giác ABCD có AB = BC, CD= DA, B= 100 độ, D= 70 độ. Tính góc A và góc C
cho tứ giác ABCD có AB=a; BC=b; CD=c; DA=d (a,b,c,d > 0 thỏa \(a^2+b^2+c^2+d^2=\left(a+c\right)\left(b+d\right)\)
a) tứ giác ABCD có gì đặc biệt?
b) nếu cho thêm giả thiết AC*BD=ab+cd khi đó tính các góc của ABCD
a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi
Đúng 0
Bình luận (0)
Tứ giác ABCD có AB = BC, CD = DA.
a) Chứng minh BD là đường trung trực của AC.
b) Cho biết góc B = 100 độ, góc D = 70 độ. Tính góc A và góc C
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D 1 : 2 : 3 : 4
a) Tính các góc của tứ giác ABCD
b) Chứng minh: AB // CD
c) Gọi giao điểm của AD cắt BC E. Tính các góc của ΔCDE
Bài 2: Cho tứ giác ABCD có ∠C 80^0 ; D 70^0 . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIB.
Bài 3: Cho tứ giác ABCD có AB BC; CD DA.
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho biết ∠B 100^0 ; D 70^0 . Tính ∠A và C
Đọc tiếp
Bài 1: Cho tứ giác ABCD biết góc A : B : C : D = 1 : 2 : 3 : 4
a) Tính các góc của tứ giác ABCD
b) Chứng minh: AB // CD
c) Gọi giao điểm của AD cắt BC = E. Tính các góc của ΔCDE
Bài 2: Cho tứ giác ABCD có ∠C = \(80^0\) ; D = \(70^0\) . Các tia phân giác của các góc A và B cắt nhau tại I. Tính AIB.
Bài 3: Cho tứ giác ABCD có AB = BC; CD = DA.
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho biết ∠B = \(100^0\) ; D = \(70^0\) . Tính ∠A và C
Cho tứ giác ABCD có AB= BC; CD = DA
a) Chứng minh BD là đường trung trức của AC
b) Cho \(\widehat{B}\) = 100 độ, \(\widehat{D}\)= 80 độ. Tính \(\widehat{A}\) và \(\widehat{C}\)
a) Ta có : AB=BC và CD=DA (đề bài)
⇒ BD là đường trung trực của AC
b) Ta có : AB=BC (đề bài)
⇒ Δ ABC cân tại B
⇒ Góc BAC = Góc BCA
Tương tự ta chứng minh Góc DAC = Góc DCA (CD=AD...)
mà Góc A = Góc BAC + Góc DAC
Góc C = Góc BCA+ Góc DCA
⇒ Góc A = Góc C
mà A + B + C +D =360; B=100o ; D=80o
⇒ A + C =360 - (100 + 80) = 240
⇒ A = C = 240 : 2 = 120o
Đúng 0
Bình luận (0)