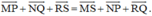
Cho 6 điểm M, N, P, Q, R, S bất kì. Chứng minh rằng : 

\(\overrightarrow{MP}+\overrightarrow{NQ}+\overrightarrow{RS}=\overrightarrow{MS}+\overrightarrow{NP}+\overrightarrow{RQ}\)

Cho m và n là 2 số bất kỳ.

Chứng minh rằng : \(m^2+n^2+2\ge2\left(m+n\right)\)

Cho n STN bất kỳ ( m>5) chứng minh rằng có thể tìm được 2 STN bất kỳ có hiệu chia hết cho 6

Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của AC, AB; D là một điểm bất kỳ trên BC. Điểm P nằm trên BF sao cho DP//CF. Điểm Q nằm trên CE sao cho DQ//BE. Đoạn PQ cắt BE ở R và cắt CF ở S. Chứng minh RS=PQ/3

1/ Cho một điểm sáng S và một điểm M bất kỳ đặt trước gương phẳng G .
a/ Vẽ ảnh S' của S cho bởi gương . Chứng minh rằng S' đối xứng với S qua mặt gương
b/ Vẽ tia sáng pahts ra từ S₁ pahnr xạ lên trên gương rồi đi qua M

c/ Chứng minh rằng trong vô số các đường đi từ S đến gương rồi đến M thì đường mà ánh sáng đi theo là ngắn nhất

cho tứ giác abcd gọi m n p q lần lượt là trung điểm của ab bc cd da gọi e là điểm bất kỳ nằm ngoài tứ giác,f là điểm đối xứng vs e qua m g là điểm đối xứng vs f qua q ,h là điểm đối xứng vs g qua p chứng minh rằng e là điểm đối xứng vs h qua n

Bài tập 05. Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ nằm trên đường chéo AC. Gọi M, N lần lượt là hình chiếu của E xuống AB, CD.
i. Chứng minh rằng: M, E, N thẳng hàng.
ii. Gọi BE cắt CD tại R. Cmr: ME-CR=NE-CD.
iii. Gọi P là hình chiếu của E xuống AD. Chứng minh
rằng: EM AD EP AB
ME AC AM
NE EC NC

3. Cho đường tròn
O R; 
. Gọi B là điểm đối xứng của O qua điểm A bất kỳ trên
O
. Từ B vẽ các tiếp

tuyến BM và BN với đường tròn (M, N là các tiếp điểm). Gọi H là giao điểm của OA và MN.
1) Chứng minh rằng
BMN
đều. 2) Tứ giác AMON là hình gì? Vì sao?

3) Tính BM và OH theo R.