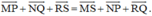Các câu hỏi tương tự
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
cho tứ giác ABCD nội tiếp đường tròn (O). Đường thẳng d bất kì trong mặt phẳng cắt AB, CD, AC, BD, AD, BC lần lượt tại M, N, P, Q, R, S và cắt đường tròn (O) tại U, V. Chứng minh rằng nếu 2 trong 3 đoạn MN, PQ, RS có cùng trung điểm thì cả 4 đoạn MN, PQ, RS, UV có cùng trung điểm
Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
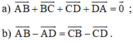
CHỨNG MINH BẰNG 3 cách khác nhau: (khác sgk)
Với 4 điểm bất kỳ A,B,C,D ta luôn có \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC}\)
Trong mặt phẳng tọa độ oxy cho A(4;0),B(8;0)C(0;4)D(0;6)m92;3)
a/ chứng minh rằng : B,C,M thẳng hàng và A,D,m thẳng hàng
b/ Gọi P,Q,R lần lượt là trung điểm các đoạn thẳng OM,AC và BD.CMR; 3 điểm P,Q,R thẳng hàng
1. Cho tập Xleft{1,2,...,nright}, ở đó ninℕ^∗. Chứng minh rằng số các tổ hợp gồm r phần tử của X không chứa bất kì 2 phần tử liên tiếp nào là C^r_{n-r+1} với 0le rle n-r+1
2. Một hoán vị x_1,x_2,...,x_{2n} của tập left{1,2,...,2nright} (với ninℕ) được gọi là có tính chất T nếu left|x_i-x_{i+1}right|n với ít nhất một chỉ số i thuộc tập left{1,2,...,2n-1right}. Chứng minh rằng với mọi n , có nhiều hoán vị có tính chất T hơn là những hoán vị không có tính chất T.
Giúp mình làm những bài này vớ...
Đọc tiếp
1. Cho tập \(X=\left\{1,2,...,n\right\}\), ở đó \(n\inℕ^∗\). Chứng minh rằng số các tổ hợp gồm \(r\) phần tử của \(X\) không chứa bất kì 2 phần tử liên tiếp nào là \(C^r_{n-r+1}\) với \(0\le r\le n-r+1\)
2. Một hoán vị \(x_1,x_2,...,x_{2n}\) của tập \(\left\{1,2,...,2n\right\}\) (với \(n\inℕ\)) được gọi là có tính chất \(T\) nếu \(\left|x_i-x_{i+1}\right|=n\) với ít nhất một chỉ số \(i\) thuộc tập \(\left\{1,2,...,2n-1\right\}\). Chứng minh rằng với mọi \(n\) , có nhiều hoán vị có tính chất \(T\) hơn là những hoán vị không có tính chất \(T\).
Giúp mình làm những bài này với. Mình nghĩ mãi vẫn không nghĩ ra lời giải nào thỏa đáng. Mình cảm ơn trước.
cho hình chữ nhật abcd có cạnh ab = 8, bc = 6 lấy điểm m bất kì , chứng minh rằng vectơ ac + bm = am + bc
Cho tam giác nhọn ABC nội tiếp đường tròn (O). M, N là hai điểm thuộc cung nhỏ
A
C
⏜
sao cho MN song song với AC và tia BM nằm giữa hai tia BA, BN. BM giao AC tại P.Gọi Q là một điểm thuộc cung nhỏ
B
C
⏜
sao cho PQ vuông góc với BC. QN giao AC tại R2). Chứng minh rằng BR vuông góc với AQ
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn (O). M, N là hai điểm thuộc cung nhỏ A C ⏜
sao cho MN song song với AC và tia BM nằm giữa hai tia BA, BN. BM giao AC tại P.
Gọi Q là một điểm thuộc cung nhỏ B C ⏜ sao cho PQ vuông góc với BC. QN giao AC tại R
2). Chứng minh rằng BR vuông góc với AQ
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.