a) Ta có:
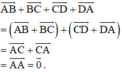
b) Áp dụng quy tắc trừ hai vec tơ ta có:

a) Ta có:
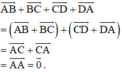
b) Áp dụng quy tắc trừ hai vec tơ ta có:

CHỨNG MINH BẰNG 3 cách khác nhau: (khác sgk)
Với 4 điểm bất kỳ A,B,C,D ta luôn có \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC}\)
Cho tứ giác ABCD nội tiếp đường tròn (O;R). Gọi a, b, c, d lần lượt là độ dài các cạnh AB, BC, CD, DA ; G là trọng tâm của tứ giác, T là điểm đối xứng của G qua O. Chứng minh rằng TA + TB +TC +TD \(\ge4R\)
Cho tứ giác ABCD có hai đường chéo AC vuông góc với BD. Chứng minh rằng:
AB2 + CD2 = AD2 + BC2
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi 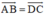
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
Chứng minh rằng với mọi tam giác ABC, AB = c, BC = c, CA = b. Ta luôn có:
\(\sqrt{x}+\sqrt{y}+\sqrt{z}\le\sqrt{\frac{a^2+b^2+c^2}{2R}}\) với x, y, z là khonagr cách từ điểm M bất kì nằm bên trong tam giác ABC đến ba cạnh BC, CA, AB theo thứ tự.
Cho tứ giác ABCD. Chứng minh rằng nếu |vecto AD + vecto BC| = |vecto AB + vecto DC| thì AC vuông góc với BD
Chứng minh rằng trong tam giác ABC ta luôn có a+b.cosC+c.CosB
Chứng minh với mọi tập A, B, C bất kì ta luôn có A\(B hợp C) =(A\B) giao (A\C)