Cho hình 39.
So sánh góc DBC và góc DCB.
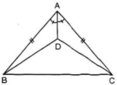
Hình 39
Cho hình 39 :
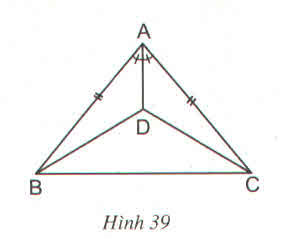
a) Chứng minh \(\Delta ABD=\Delta ACD\)
b) So sánh góc DBC và góc DCB
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=>
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a,
Xét tam giác ABD và tam giác ACD có :
AD là cạnh chung
góc A1 = góc A2
AB=AC
Do đó: tam giác ABD - tam giác ACD ( c-g-c )
b,
từ tam giác ABD= tam giác ACD (c-g-c)
suy ra đc BD=BC
suy ra dc tam giác DBC là tam giác cân
suy ra dc góc DBC=góc DCB
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
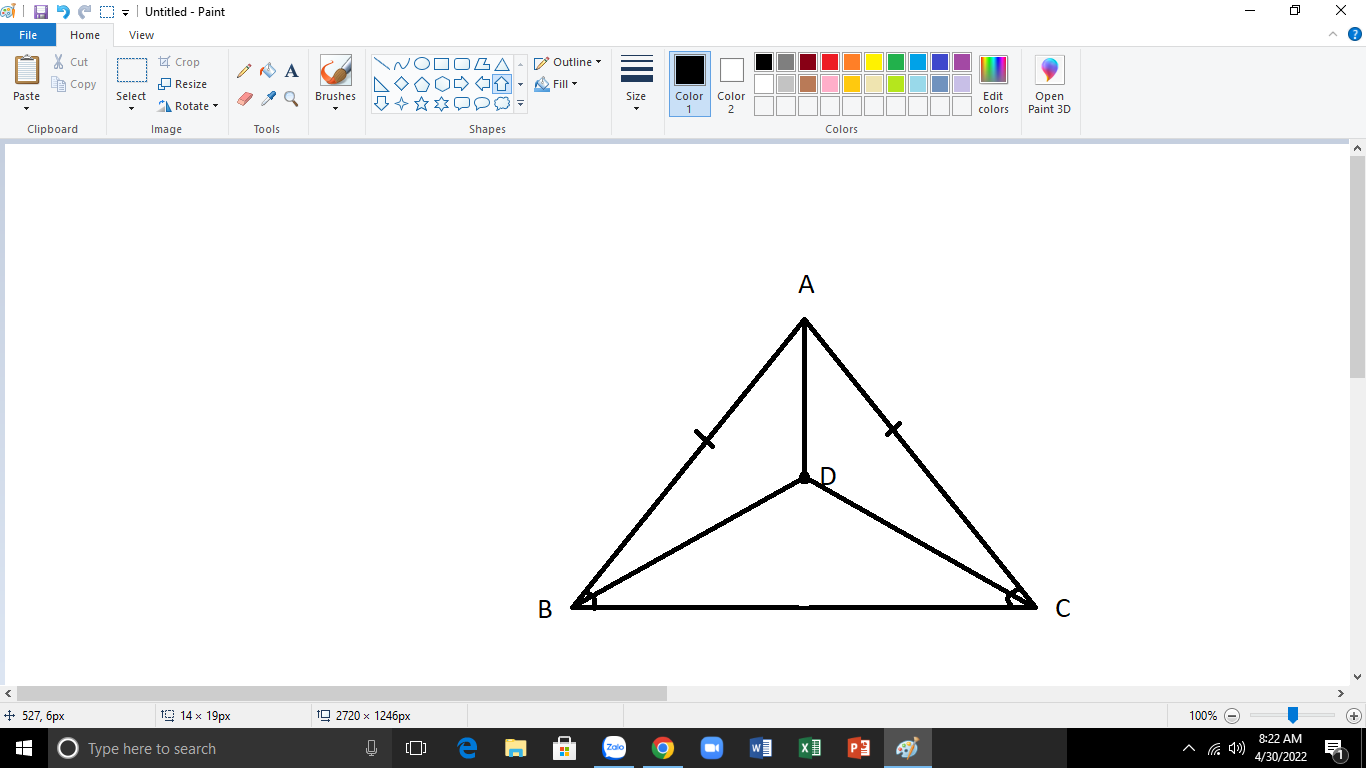
\(\text{a)Xét }\Delta ABD\text{ và }\Delta ACD\text{ có:}\)
\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
\(AD\text{ chung}\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Ta có:}\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)
\(\text{Mà }\widehat{ABD}=\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
cho tam giác abc cân tại a điểm d nằm trong tam giác sao cho bad=cad
a, CM rằng tam giác abd = tam giác acd
b,so sánh góc dbc và góc dcb
Đây nha:
a. Xét tam giác ABD và tam giác ACD có:
góc BAD = góc BAC (gt)
AD chung
AB = AC (tam giác ABC cân)
=> tam giác ABD = tam giác ACD (cgc)
b. Gọi E là trung điểm của BC
Có: góc BAC = góc BAD + góc CAD mà góc BAD = góc CAD
=> AD là đường phân giác
Lại có: tam giác ABC cân tại A => AD đồng thời là đường trung trực của tam giác ABC
Do đó: DE là đường trung trực cũng là đường phân giác của tam giác BDC.
=> DE vuông với BC tại E; góc BDE = góc CDE
Xét tam giác BDE và tam giác CDE vuông tại E có:
DE chung
góc BDE = góc CDE (cmt)
=> tam giác BDE = tam giác CDE (ch-cgv)
=> góc DBC = góc DCB (2 góc tương ứng)
Cho ∆ABC có AB < AC. Vẽ AH vuông góc BC tại H.
a. Chứng minh: BH < HC.
b. Trên tia đối của tia HA lấy điểm D. So sánh góc DBC và góc DCB?
Giúp e làm bài đó nka mấy anh/chị =)) <3
a: Xét ΔBAC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔDBC có BH<CH
mà BH là hình chiếu của DB trên BC
và CH là hình chiếu của DC trên BC
nên DB<DC
=>\(\widehat{DCB}< \widehat{DBC}\)
Cho tam giác ABC có góc C < góc B < 90 độ. Kẻ AH \(\perp\)vuông góc với BC ( H thuộc BC). Gọi D là điểm bất kỳ nằm giữa A và H. So sánh :
a. HB và HC.
b. góc DBC và góc DCB.
c. góc ADB và góc ADC.
Bài 1. Cho hình vẽ bên biết AOC+BOD=140.TÍnh AOC,COB,BOD,DOA
Bài 3. Đường thẳng xx' cắt dường thẳng yy' từ O. Vẽ tia phân giác Ot của góc xOy
a) Gọi Ot' là tia đôi của tia Ot. So sánh xOt' và t'Oy.
b) Vẽ tia phân giác Om của góc xOy'. Tính góc mOt
Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o
1.
Ta có: ∠AOC+ ∠BOD= 140o
Mà 2 góc này là 2 góc đối đỉnh
⇒ ∠AOC= ∠BOD= 70o
Ta lại có:
∠AOD+ ∠DOB= 180o ( Hai góc kề bù )
⇒ ∠AOD= 110o
Do BOC và AOD là 2 góc đối đỉnh
⇒ ∠BOC= 110o\(^{ }\)
Vậy...
cho hình vẽ.Biết xx'//yy' và góc xAB=58 độ.Tính số đo góc y'Bt'
cho hình bình hành ABCD có góc A là góc tù kẻ AH và CK vuông góc với vuông góc với đường chéo BD.
a)chứng minh tứ giác AHCK là hình bình hành.
''lập luận chặt chẽ hộ mình nha''
Cho hình vẽ :
O'x' song song với Ox , O'y cắt Ox tại k . Tính góc x'O'y' và góc x'O'k theo góc O