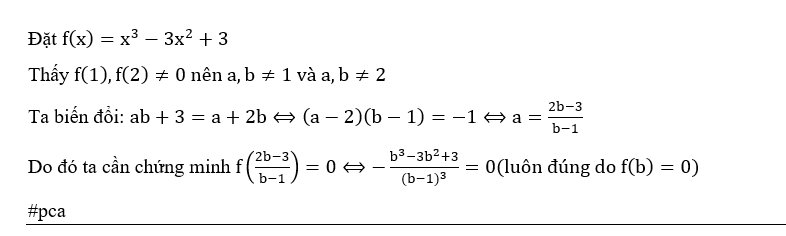Chứng minh rằng phương trình x 3 + 6 x + 1 - 2 = 0 có nghiệm dương

Những câu hỏi liên quan
a) giải phương trình: 8x-3=5x+12
b) giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{8-11x}{4}\)< 13
c) Chứng minh rằng: (\(\dfrac{x}{x^2-36}\)- \(\dfrac{x-6}{x^2+6x}\)): \(\dfrac{2x-6}{x^2+6x}\)+ \(\dfrac{x}{6-x}\)= 1
a:=>3x=15
=>x=5
b: =>8-11x<52
=>-11x<44
=>x>-4
c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)
\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)
Đúng 1
Bình luận (0)
Cho hai phương trình x 2 - 5 x + 6 = 0 (1) và x + (x - 2)(2x + 1) = 2 (2)
Chứng minh rằng hai phương trình có chung nghiệm là x = 2.
Thay x = 2 vào vế trái phương trình (1):
2 2 – 5.2 + 6 = 4 – 10 + 6 = 0
Vế trái bằng vế phải, vậy x = 2 là nghiệm của phương trình (1).
Thay x = 2 vào vế trái phương trình (2):
2 + (2 - 2) (2.2 + l) = 2 + 0 = 2
Vế trái bằng vế phải, vậy x = 2 là nghiệm của phương trình (2).
Đúng 0
Bình luận (0)
x2−5x+6=0x2−5x+6=0 (1)
x+(x−2)(2x+1)=2x+(x−2)(2x+1)=2 (2)
a. Chứng minh rằng hai phương trình có nghiệm chung là x = 2
b. Chứng minh rằng x = 3 là nghiệm của (1) nhưng không là nghiệm của (2)
c. Hai phương trình đã cho có tương đương với nhau không, vì sao ?
a. Thay x = 2 vào vế trái của phương trình (1), ta có:
22 – 5.2 + 6 = 4 – 10 + 6 = 0
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (1).
Thay x = 2 vào vế trái của phương trình (2), ta có:
2 + (2 – 2)(2.2 +1) = 2 + 0 = 2
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (2).
Vậy x = 2 là nghiệm chung của hai phương trình (1) và (2).
b. Thay x = 3 vào vế trái của phương trình (1), ta có:
32 – 5.3 + 6 = 9 – 15 + 6 = 0
Vế trái bằng vế phải nên x = 3 là nghiệm của phương trình (1).
Thay x = 3 vào vế trái của phương trình (2), ta có:
3 + (3 – 2)(2.3 + 1) = 3 + 7 = 10 ≠ 2
Vì vế trái khác vế phải nên x = 3 không phải là nghiệm của phương trình (2).
Vậy x = 3 là nghiệm của phương trình (1) nhưng không phải là nghiệm của phương trình (2).
c. Hai phương trình (1) và (2) không tương đương nhau vì x = 3 không phải là nghiệm chung của hai phương trình.
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình :
\(x^6-x^5+x^4-x^3+x^2-x+\frac{3}{4}=0\) vô ngiệm
+) Nếu x<0 ta có
x^6>0, x^5<0, x^4>0, x^3<0,x^2>0, x<0=>x^6-x^5+x^4-x^3+x^2-x > 0=>x^6-x^5+x^4-x^3+x^2-x+3/4>0(trái với đề bài)
+)Nếu x > hoặc =0 thì x^6>x^5, x^4>x^3, x^2>x, 3/4>0 =>x^6-x^5+x^4-x^3+x^2-x+3/4>0(trái với đề bài)
Vậy phương trình trên vô nghiệm
Đúng 0
Bình luận (0)
Bài 3: (1,5 điểm)
Cho phương trình: x2 – (m + 5)x + 2m + 6 = 0 (x là ẩn số)
a) Chứng minh rằng phương trình trên luôn có hai nghiệm x1, x2 với mọi m.
b) Tìm m để X12 + x22 = 13
a, Ta có:
\(\Delta=\left[-\left(m+5\right)\right]^2-4\left(2m+6\right)\\ =m^2+10m+25-8m-24\\ =m^2+2m+1\\ =\left(m+1\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm x1,x2
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=m+5\\x_1x_2=2m+6\end{matrix}\right.\)
\(x^2_1+x^2_2=13\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\\ \Leftrightarrow\left(m+5\right)^2-2\left(2m+6\right)=13\\ \Leftrightarrow m^2+10m+25-4m-12-13=0\\ \Leftrightarrow m^2+6m=0\\ \Leftrightarrow m\left(m+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-6\end{matrix}\right.\)
Đúng 4
Bình luận (1)
cho 6 số thực a1<a2<a3<a4<a5<a6. Chứng minh rằng phương trình (x-a1)(x-a3)(x-a5)+(x-a2)(x-a4)(x-a6)=0 có đúng 3 nghiệm phân biệt.
Đặt \(f\left(x\right)=\left(x-a_1\right)\left(x-a_3\right)\left(x-a_5\right)+\left(x-a_2\right)\left(x-a_4\right)\left(x-a_6\right)\)
\(f\left(a_1\right)=\left(a_1-a_2\right)\left(a_1-a_4\right)\left(a_1-a_6\right)< 0\)
\(f\left(a_2\right)=\left(a_2-a_1\right)\left(a_2-a_3\right)\left(a_2-a_5\right)>0\)
\(f\left(a_4\right)=\left(a_4-a_1\right)\left(a_4-a_3\right)\left(a_4-a_5\right)< 0\)
\(f\left(a_6\right)=\left(a_6-a_1\right)\left(a_6-a_3\right)\left(a_6-a_5\right)>0\)
\(\Rightarrow f\left(x\right)\) có nghiệm thuộc các khoảng \(\left(a_1,a_2\right);\left(a_2,a_4\right);\left(a_4,a_6\right)\)
mà bậc cao nhất của f(x) là 3 nên f(x) có tối đa 3 nghiệm
=> dpcm
Đúng 1
Bình luận (0)
Bài 4:Cho phương trình ẩn x: x2 - (m + 3)x + m = 0
a) Chứng minh rằng với mọi giá trị của m phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình có 2 nghiệm Phân biệt x1, x2 thỏa mãn hệ thức:
x12 + x22 = 6
a) \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\\ =m^2+6m+9-4m\\ =m^2+2m+9\\ =\left(m+1\right)^2+8>0\forall m\)
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.
b) Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow\left(m+3\right)^2-2m=6\\ \Leftrightarrow m^2+6m+9-2m=6\\ \Leftrightarrow m^2+4m+3=0\\ \Leftrightarrow\left(m+1\right)\left(m+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy \(m\in\left\{-1;-3\right\}\) là các giá trị cần tìm.
Đúng 1
Bình luận (0)
a, Ta có: \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\)
\(=m^2+6m+9-4m\)
\(=m^2+2m+9\)
\(=m^2+2m+1+8\)
\(=\left(m+1\right)^2+8\)
Lại có: \(\left(m+1\right)^2\ge0\forall m\Rightarrow\left(m+1\right)^2+8\ge8\forall m\)
Vậy phương trình luôn có 2 nghiêm phân biệt
b, Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1+x_2=m\end{matrix}\right.\)
Theo bài ra:
\(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(m+3\right)^2-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m-6=0\)
\(\Leftrightarrow m^2+4m+3=0\)
\(\Leftrightarrow m^2+m+3m+3=0\)
\(\Leftrightarrow\left(m^2+m\right)+\left(3m+3\right)=0\)
\(\Leftrightarrow m\left(m+1\right)+3\left(m+1\right)=0\)
\(\Leftrightarrow\left(m+1\right)\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\m+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy với m=-1 hoặc m=-3 thì phương trinh trên thỏa mãn hệ thức
Đúng 1
Bình luận (0)
6. Biết rằng phương trình x 3 −3x 2 +3 = 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 = a+2b.
6. Biết rằng phương trình x 3 −3x 2 +3 = 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 = a+2b.
Cho phương trình x2-(2m-3)x+m2-3m=0
a)Chứng minh rằng phương trình có nghiệm với mọi m
b)Xác định m để phương trình có nghiệm x1;x2 thỏa mãn 1<x1<x2<6