Cho cos a = 4 5 với 0 < α < π 2 .Tính sinα.
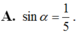
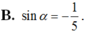
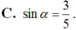
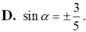
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Cho cos α=-2/5 và π<α<3π/2. tính tanα, sinα ,cotα
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{\sqrt{21}}{5}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\dfrac{\sqrt{21}}{5}}{-\dfrac{2}{5}}=\dfrac{\sqrt{21}}{2}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{2}{\sqrt{21}}\)
Cho sinα = 5 / 4 . Giá trị cos(α + π/2) là
![]()
cos(α+ π/2) = cos(α- π/2+ π) = - cos(α- π/2).
Vậy đáp án là D.
Tính cos(α-π/3) biết sinα=3/5 và π/2
Lời giải:
$\cos^2 a=1-\sin^2a=1-(\frac{3}{5})^2=\frac{16}{25}$
$\Rightarrow \cos a=\pm \frac{4}{5}$
Ta có:
\(\cos (a-\frac{\pi}{3})=\cos a\cos \frac{\pi}{3}-\sin a\sin \frac{\pi}{3}\)
\(=\frac{1}{2}\cos a-\frac{3\sqrt{3}}{10}=\frac{1}{2}.\pm \frac{4}{5}-\frac{3\sqrt{3}}{10}\)
Chứng minh rằng với mọi α, ta luôn có
cos(α + π/2) = -sinα
Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
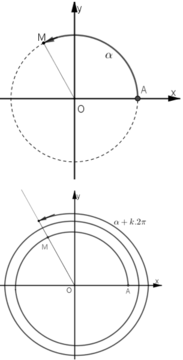
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
1. Cho α + β + f = π . CM:
a1) sinα + sinβ +sinf = 4.cos\(\dfrac{\alpha}{2}\) .cos\(\dfrac{\beta}{2}\). cos\(\dfrac{f}{2}\)
a2) cosα + cosβ +cosf = 1+ 4sin\(\dfrac{\alpha}{2}\).sin\(\dfrac{\beta}{2}\).sin\(\dfrac{f}{2}\)
Các bạn giúp mình với ạ
1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)
Cho góc α thỏa mãn sin2α = -4 / 5 và 3π / 4 < α < π. Tính P = sinα - cosα.
3/4pi<a<pi
=>sin a>0; cosa<0
sin2a=-4/5
=>2*sina*cosa=-4/5
=>sina*cosa=-2/5
(sina-cosa)^2=sin^2a+cos^2a-2*sina*cosa=1+4/5=9/5
=>sin a-cosa=3/căn 5