Cho cấp số cộng ( u n ) có d= -2 và S 8 = 72 . Tìm số hạng đầu tiên u 1 ?
A. 16
B. – 16
C. 4
D. 8
Cho cấp số cộng (un) có d = -2 và S8 = 72. Số hạng đầu tiên của cấp số cộng bằng
A. - 1 16
B. 1 16
C. 16
D. -16.
Cho cấp số cộng (un) có d = -2 và S8 = 72. Số hạng đầu tiên của cấp số cộng bằng
A. - 1 16
B. 1 16
C. 16
D. -16
Chọn đáp án C.
Có S 8 = 8 2 ( 2 u 1 + ( 8 - 1 ) d )
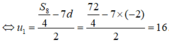
cho cấp số cộng (Un) có công sai d= -2 và Sn =72.Tính U1
Đề bài sai, không thể tính \(u_1\) (sẽ có vô số giá trị \(u_1\) thỏa mãn)
cho cấp số cộng (u\(_n\)) có công sai d khác 0 và cấp số nhân (v\(_n\)) có công bội q là số dương thỏa mãn \(u_1=v_1=-2\); \(u_2=v_2\); \(u_3=v_3+8\). tính tổng d+q
\(u_2=u_1+d=-2+d\) ; \(v_2=v_1q=-2q\)
\(u_2=v_2\Rightarrow-2+d=-2q\Rightarrow d=2-2q\)
\(u_3=v_3+8\Leftrightarrow-2+2d=-2q^2+8\)
\(\Leftrightarrow-2+2\left(2-2q\right)=-2q^2+8\)
\(\Leftrightarrow2q^2-4q-6=0\Rightarrow\left[{}\begin{matrix}q=-1\Rightarrow d=4\\q=3\Rightarrow d=-4\end{matrix}\right.\)
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng (Un). Tính
a) \(S=\frac{1}{U_1U_2}+\frac{1}{U_2U_3}+...+\frac{1}{U_{n-1}U_n}\) theo d , U1 , Un
b) \(S=U_1^2+U_2^2+...+U_n^2\) theo d , U1 , Un
S= u1.u1 + u2.u2+...+un.un
S = u1.(u2 - d) + u2.(u3 - d)+...+un(un+1 - d)
S = u1.u2 + u2.u3 +...+un.un+1-d(u1+u2+...+un)
Đặt A = u2.u3 + u3.u4+...+un.un+1
3d.A = u2.u3.(u4-u1) + u3.u4.(u5-u2)+...+un.un+1.(un+2-un-1)
3d.A = u2.u3.u4 - u1.u2.u3 + u3.u4.u5 - u2.u3.u4+...+un.un+1.un+2 - un-1.un.un+1
3d.A = un.un+1.un+2 - u1.u2.u3
3d.A = (u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)
A = [(u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)]/(3.d)
S = A + u1.(u1 + d) + d[2.u1+(n-1).d].n/2
1) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2\) và \(u_7=-10\) công sai của cấp số cộng là
2) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=1\) và d = 2 tổng \(S_{10}=u_1+u_2+u_3...+u_{10}\) bằng
3) cho cấp số cộng \(\left(u_n\right)\) có số hạng đầu \(u_1=3\) và d = 2. Tổng của 2019 số hạng đầu bằng
4) cho cấp số cộng 2;5;8;11;14... công sai của cấp số cộng đã cho bằng
5) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2\) và d = 9 khi đó số 2018 là số hạng thứ mấy trong dãy
6) cho cấp số cộng \(\left(u_n\right)\) có số hạng đầu \(u_1=3\) và d = 2
\(Bài.1:\\ u_7=u_1+6d\\ \Leftrightarrow-10=2+6d\\ \Rightarrow6d=-10-2=-12\\ Vậy:d=\dfrac{-12}{6}=-2\\ Bài.2:S_{10}=10.u_1+\dfrac{10.\left(10-1\right)}{2}.d=10.1+\dfrac{10.9}{2}.2=100\\ Bài.3:S_{2019}=2019.u_1+\dfrac{2019.\left(2019-1\right)}{2}.d\\ =2019.3+\dfrac{2019.2018}{2}.2=2019.2021=4080399\)
Bài 4:
\(d=u_2=u_1=5-2=3\)
Bài 5:
\(u_n=u_1+\left(n-1\right)d\\ \Leftrightarrow2018=2+\left(n-1\right).9\\ \Leftrightarrow2+9n-9=2018\\ \Leftrightarrow9n=2018-2+9\\ \Leftrightarrow9n=2025\\ \Leftrightarrow n=\dfrac{2025}{9}=225\)
Vậy: 2018 là số hạng thứ 225 của dãy
Bài 6:
Đề chưa có yêu cầu
4: d=u2-u1=3
5: Đặt 2018=2+(n-1)*9
=>9(n-1)=2016
=>n-1=224
=>n=225
=>2018 là số thứ 225
3:
\(S_{2019}=2019\left(\dfrac{2\cdot3+2018\cdot2}{2}\right)=4080399\)
2:
\(S_{10}=\dfrac{10\cdot\left(2\cdot1+9\cdot2\right)}{2}=10\left(1+9\right)=100\)
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
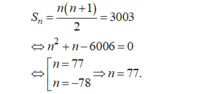
a. Tìm hệ số của x trong khai triển ( x2 - \(\dfrac{2}{x}\) )8
b. Cho cấp số cộng (un ) có u12= 17 , S12 = 72 . Xác định giá trị của u1 , công sai d.
a, \(\left(x^2-\dfrac{2}{x}\right)^8=\sum\limits^8_{k=0}C^k_8.x^{16-2k}.\dfrac{\left(-2\right)^k}{x^k}\)
\(=\sum\limits^8_{k=0}C^k_8.\left(-2\right)^k.x^{16-3k}\)
\(16-3k=1\Leftrightarrow k=5\)
\(\Rightarrow\) Hệ số của x trong khai triển là \(C^5_8.\left(-2\right)^5=-1792\)
b, \(\left\{{}\begin{matrix}u_{12}=17\\S_{12}=72\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+11d=17\\\dfrac{12.\left(u_1+u_{12}\right)}{2}=72\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+11d=17\\u_1+17=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=2\\u_1=-5\end{matrix}\right.\)