Hai hệ phương trình k x + 3 y = 3 - x + y = 1 ; x + y = 1 - x + y = 1 là tương đương khi k bằng?
A. k = -3
B. k = 1
C. k = 3
D. k = -1
Cho hệ phương trình: \(\hept{\begin{cases}kx-y=2\\x+ky=1\end{cases}}\)
a, Giải hệ phương trình khi k = 5
b, Tìm k để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện \(x+y=\frac{-3}{k^2+1}\)
cho hệ phương trình x + y = 3k - 2
2x - y = 5 với k là tham số
giải hệ phương trình khi k = 1
tìm k để hệ phương trình có nghiệm ( x ; y) sao cho x^2 - y - 5/ y + 1 = 4
Thay k=1 và HPT ta có:
\(\left\{{}\begin{matrix}x+y=3.1-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x+y=1\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\3y=-3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y) = (2;-1)
b) tìm k để hệ phương trình có nghiệm ( x ; y) sao cho \(x^2-y-\dfrac{5}{y}+1=4\)
\(\left\{{}\begin{matrix}x+y=3k-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-\left(3k-2-x\right)=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-3k+2+x=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\3x=3k+3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\x=k+1\end{matrix}\right.\)
Ta có \(\text{ x= k+1 }=>y=2k-3\) (*)
Thay vào biểu thức đã cho ở đề bài ta có :
\(x^2-y-\dfrac{5}{y}+1=4\)
⇔\(\left(k+1\right)^2-2k+3-\dfrac{5}{2k-3}+1=4\)
⇔\(k^2+2k+1-2k+3-\dfrac{5}{2k-3}+1=4\)
Sau một hồi bấm máy tính Casio thì ra k=2
Vậy k=2 thì Thỏa mãn yêu cầu đề bài
Lần sau bạn dùng Latex đánh đề bài cho dễ nhìn nha, mình sợ chép lại đề bài bị sai @@
Cặp số (x; y) = (1; 3) là nghiệm của hệ phương trình bậc nhất hai ẩn nào trong các hệ phương trình sau:
A. x - y = - 2 x + y = 4
B. 2 x - y = 0 x + y = 4
C. 2 x + y = 4 x + y = 4
D. x 2 + y 2 = 10 x - y = 2
Đáp án A
Phương án D không phải là hệ phương trình bậc nhất hai ẩn nên loại D

Cặp số (x; y) = (1; 3) là nghiệm của hệ phương trình bậc nhất hai ẩn nào trong các hệ phương trình sau:
A. x − y = − 2 x + y = 4
B. 2 x − y = 0 x + y = 4
C. x + y = 4 2 x + y = 4
D. x 2 + y 2 = 10 x − y = 2
Hệ phương trình có chứa phương trình bậc hai là hệ phương trình ở đáp án D nên loại D
+ Với hệ phương trình A:
x − y = − 2 x + y = 4 ⇒ 1 − 3 = − 2 1 + 3 − 4 ⇔ − 2 = − 2 4 = 4 (luôn đúng) nên (1; 3) là nghiệm của hệ phương trình x − y = − 2 x + y = 4
+ Với hệ phương trình B: 2 x − y = 0 x + y = 4
Thay x = 1; y = 3 ta được 2.1 − 3 = 0 1 + 3 = 4 ⇔ − 1 = 0 1 + 3 = 4 (vô lý) nên loại B.
+ Với hệ phương trình C: x + y = 4 2 x + y = 4
Thay x = 1; y = 3 ta được 1 + 3 = 4 2.1 + 3 = 4 ⇔ 4 = 4 5 = 4 (vô lý) nên loại C.
Đáp án:A
Cho hệ phương trình
\(\begin{cases} (k - 1)x + y = 3k - 4\\ x + (k - 1)y = k - 1 \end{cases}\)
Tìm k ϵ Z để hệ phương trình có nghiệm (x; y) sao cho x, y ϵ Z
Cho hệ phương trình:
\(\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\x^3+y^3+\dfrac{1}{x^3}+\dfrac{1}{y^3}=15m-25\end{matrix}\right.\) ( m là tham số).
a, Giải hệ phương trình trên khi m = 3.
b, Tìm m để hệ phương trình trên có nghiệm (x0; y0) và x0, y0 là những số dương.
Đặt \(x+\dfrac{1}{x}=a;y+\dfrac{1}{y}=b\left(\left|a\right|\ge2;\left|b\right|\ge2\right)\)
\(\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\x^3+y^3+\dfrac{1}{x^3}+\dfrac{1}{y^3}=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x^3+\dfrac{1}{x^3}\right)+\left(y^3+\dfrac{1}{y^3}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3-3\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)^3-3\left(y+\dfrac{1}{y}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3+\left(y+\dfrac{1}{y}\right)^3-3\left(x+\dfrac{1}{x}+y+\dfrac{1}{y}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3+\left(y+\dfrac{1}{y}\right)^3=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\a^3+b^3=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left(a+b\right)^3-3ab\left(a+b\right)=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\125-15ab=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\ab=9-m\end{matrix}\right.\)
\(\Rightarrow a,b\) là nghiệm của phương trình \(t^2-5t+9-m=0\left(1\right)\)
a, Nếu \(m=3\), phương trình \(\left(1\right)\) trở thành
\(t^2-5t+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\\\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+\dfrac{1}{x}=2\\y+\dfrac{1}{y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y^2-3y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3\pm\sqrt{5}}{2}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x+\dfrac{1}{x}=3\\y+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3\pm\sqrt{5}}{2}\\y=1\end{matrix}\right.\)
Vậy ...
b, \(\left(1\right)\Leftrightarrow t=\dfrac{5\pm\sqrt{4m-11}}{2}\left(m\ge\dfrac{11}{4}\right)\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5\pm\sqrt{4m-11}}{2}\\b=\dfrac{5\mp\sqrt{4m-11}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}=\dfrac{5\pm\sqrt{4m-11}}{2}\\y+\dfrac{1}{y}=\dfrac{5\mp\sqrt{4m-11}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2-\left(5\pm\sqrt{4m-11}\right)+2=0\left(2\right)\\2y^2-\left(5\mp\sqrt{4m-11}\right)+2=0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(2\right)\) có nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(5\pm\sqrt{4m-11}\right)^2-16\ge0\\\dfrac{5\pm\sqrt{4m-11}}{2}>0\\1>0\end{matrix}\right.\)
\(\Leftrightarrow...\)
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\)
B. \(\left\{ \begin{array}{l}3x + {y^3} < 0\\x + y > 3\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + 2y < 0\\{y^2} + 3 < 0\end{array} \right.\)
D. \(\left\{ \begin{array}{l} - {x^3} + y < 4\\x + 2y < 1\end{array} \right.\)
Ta thấy hệ \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn với các bất phương trình bậc nhất hai ẩn là \(x - y < 0;2y \ge 0\).
=> Chọn A.
Đáp án B loại vì \(3x + {y^3} < 0\) chứa \(y^3\).
Đáp án C loại vì \({y^2} + 3 < 0\) chứa \(y^2\).
Đáp án D loại vì \( - {x^3} + y < 4\) chứa \(x^3\).
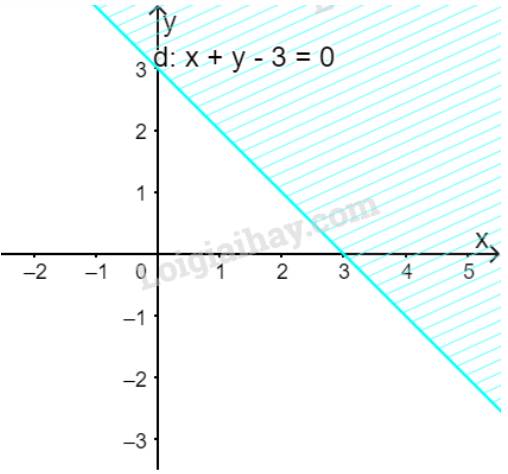
Cho hệ bất phương trình: \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\end{array} \right.\)
Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?
Tham khảo:
Vẽ đường thẳng \(d:x + y - 3 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 0 - 3 = - 3 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(d\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vẽ đường thẳng \(d': - 2x + y + 3 = 0\) đi qua hai điểm \(A(1; - 1)\) và \(B\left( {2;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 + 3 = 3 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
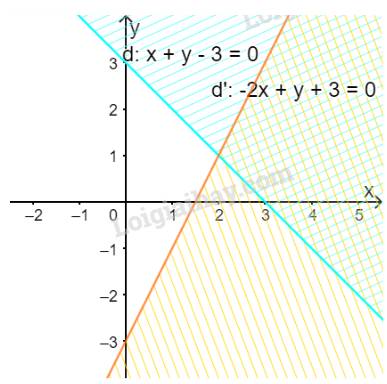
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.
Cho hệ phương trình
\(\hept{\begin{cases}\left|x\right|+x+\left|y\right|+y=2000\\\left|x\right|-x+\left|y\right|-y=k\end{cases}}\)
Trong đó K là 1 số cho trước biết rằng hệ phương trình đã cho có đúng hai nghiệm phân biệt (x;y)=(a;b) và (x;y)=(c;d)
Tổng a+b+c+d = ?
Khoa Bùi Phạm (Em làm thử)
\(\hept{\begin{cases}\left|x\right|+x+\left|y\right|+y=2000\left(1\right)\\\left|x\right|-x+\left|y\right|-y=k\left(2\right)\end{cases}}\)
Lấy (1)-(2) \(\Rightarrow2x+2y=2000-k\)
\(\Rightarrow2\left(x+y\right)=2000-k\)
Vì hệ phương trình có đúng hai no phân biệt (x;y)=(a;b) và (x;y)=(c;d)
Nên \(2\left(x+y\right)=a+b+c+d\)
Vậy \(a+b+c+d=2000-k\)
P/s: k chắc lắm -.- . Nếu có lỗi sai mong thầy/cô và các bn chỉ ra giúp em. Cảm ơn!