Tỉ số Δ y Δ x của hàm số f(x) = 2x(x - 1) theo x và Δ x là:
A. 4 x + 2 Δ x + 2
B. 4 x + 2 Δ x 2 - 2
C. 4 x + 2 Δ x - 2
D. Đáp án khác
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
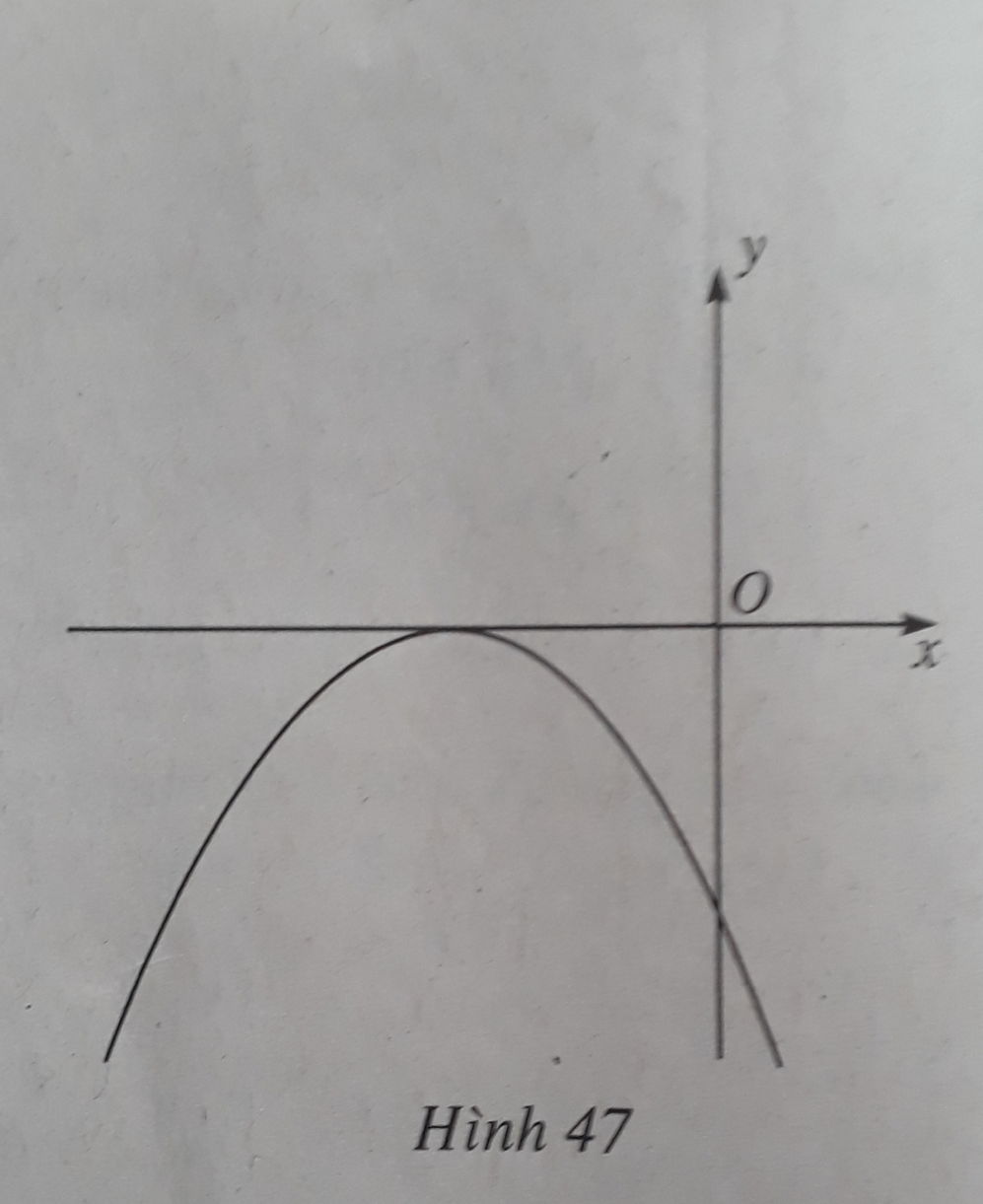
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Cho hàm số y=x2-2x-1 (P) , y=2x+1 (Δm)
a/ Tìm x để y>0, y<0, yminb/ Tìm giao điểm của (P) và đường thẳng :(Δ1): y=2x+1mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)
Cho hàm số 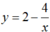 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
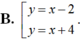
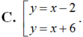
D. Không tồn tại.
Chọn C.
Đạo hàm: 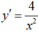
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình 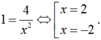
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
Phương trình tiếp tuyến với đồ thị hàm số y = x + 1 x − 1 song song với đường thẳng Δ : 2 x + y + 1 = 0 là
A. 2 x + y = 0
B. 2 x + y + 7 = 0
C. 2 x + y − 7 = 0
D. − 2 x − y − 1 = 0
Đáp án là C
y ' = − 2 x − 1 2 . Gọi M x 0 ; y 0 ∈ C là tiếp điểm.
Vì tiếp tuyến song song với đường thẳng y = − 2 x − 1 nên:
− 2 x 0 − 1 2 = − 2 ⇔ x 0 − 1 2 = 1 ⇔ x 0 = 2 ⇒ y 0 = 3 x 0 = 0 ⇒ y 0 = − 1
Phương trình tiếp tuyến cần tìm: 2 x + y − 7 = 0.
Cho ba hạt nhân X, Y và Z có số nuclôn tương ứng là A X , A Y , A Z với A X = 2 A Y = 0,5 A Z . Biết năng lượng liên kết của từng hạt nhân tương ứng là Δ E X , Δ E Y , Δ E Z với Δ E Z < Δ E X < Δ E Y . Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là
A. Y, X, Z
B. Y, Z, X
C. X, Y, Z
D. Z, X, Y
Đáp án A
Đặt
![]()
Đặt
![]()
![]()
![]()
Vậy tính bền vững của hạt nhân giảm dần theo thứu tự Y,X,Z
Cho đường thẳng Δ có phương trình \(\left\{{}\begin{matrix}x=5t\\y=-1+6t\\z=2\end{matrix}\right.\) và mặt phẳng 2x-y-4z+3=0. Hình chiếu vuông góc d' của Δ lên mặt phẳng (P) theo phương d: \(\dfrac{x-1}{2}=\dfrac{y}{4}=\dfrac{z+3}{-1}\)
Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k 1 , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k 2 . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?
Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k 1 , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k 2 . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?
cho hàm số y=f(x)=-x3+2x2-x+5 có đồ thị (C). Tìm tham số m để tiếp tuyến Δ của đồ thị (C) tại tiếp điểm A(2;3) song song với đường thẳng (d): (m2-3m-5)x-y-2m+19=0
\(\left(m^2-3m-5\right)x-y-2m+19=0\)
\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)
Ta có:
\(f'\left(x\right)=-3x^2+4x-1\)
\(f'\left(2\right)=-5\)
Phương trình tiếp tuyến tại A:
\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)
Để hai đường thẳng song song:
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
Cho Δ: 2x-y+1=0 , (C): \(x^2+y^2-2x+4y-1=0\) , \(\overrightarrow{v}\) (3,-1)
Tìm ảnh của Δ và (C) qua \(T_{\overrightarrow{v}}\)
Gọi `A(0;1)` và `B(1;3)` là 2 điểm thuộc `\Delta`
`T_(\vec v): \Delta -> \Delta'`
`<=> T_(\vec v): A(0;1) -> A'(3;0) ; B(1;3) -> B'(4;2)`
`=> \vec(A'B') (1;2)`
`=> \Delta' : 1(x-3)+2(y-0)=0 <=> x+2y-3=0`
`(C)` có: `I(1;-2)` và `R=\sqrt6 =R'`
`T_(\vec v): (C) -> (C') => T_(\vecv): I (1;-2) -> I'(4;-3)`
`=> (C'): (x-4)^2 +(y+3)^2=6`