Đơn giản biểu thức A = a 3 1 a 2 3 a 3 3 ta được:
A. A = a 5 6
B. A = a 17 18
C. A = a 5 9
D. A = a 5 16
Đơn giản biểu thức: \(A=\dfrac{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}-2}{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}+2}\)
Đơn giản biểu thức: \(A=\dfrac{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}-2}{a^3-3a+\left(a^2-1\right)\sqrt{a^2-4}+2}\)
Đơn giản biểu thức A = (1 - sin 2 x ) c o t 2 x + (1 - c o t 2 x ), ta có:
A. A = - cos 2 x
B. A = cos 2 x
C. A = sin 2 x
D. A = - sin 2 x
Đáp án: C
Ta có:
A = (1 - sin 2 x ) c o t 2 x + (1 - c o t 2 x ) = c o t 2 x - sin 2 x . c o t 2 x + 1 - c o t 2 x
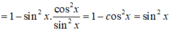
Đơn giản biểu thức A = (1 - sin2x) .cot2x + (1 - cot2x) ta được :
A. sin2x
B. 2
C. 1
D. cot2x
Đơn giản biểu thức A = (1 - sin 2 α ). c o t 2 α + (1 - c o t 2 α ) ta được :
A. A = sin 2 α
B. A = cos 2 α
C. A = - sin 2 α
D. A = - cos 2 α
Đơn giản biểu thức sau :
\(M=lg\left|\log_{\frac{1}{a^3}}\sqrt[5]{a\sqrt{a}}\right|\)
\(M=lg\left|\log_{\frac{1}{a^3}}\sqrt[5]{a\sqrt{a}}\right|=lg\left|\log_{\frac{1}{a^3}}\sqrt[5]{a.a^{\frac{1}{2}}}\right|=lg\left|\log_{\frac{1}{a^3}}\left(a^{\frac{3}{2}}\right)^{\frac{1}{5}}\right|=lg\left|\log_{a^{-3}}a^{\frac{3}{10}}\right|=lg\left|-\frac{1}{10}=lg\frac{1}{10}=-1\right|\)
Đơn giản biểu thức A = 1 - 2 b a + b a : b - a 2 ta được:
A. A = a - b
B. A = a
C. A = 1/a
D. A = a + b
1) Đơn giản biểu thức : \(A=\frac{\left(sinx+cosx\right)^2-1}{cotx-sinx.cosx}\)
2) Đơn giản biểu thức : \(N=\left(\frac{sinx+tanx}{cosx+1}\right)^2+1\)
\(A=\frac{sin^2x+cos^2x+2sinx.cosx-1}{\frac{cosx}{sinx}-sinx.cosx}=\frac{2sinx^2x.cosx}{cosx-sin^2x.cosx}=\frac{2sin^2x.cosx}{cosx\left(1-sin^2x\right)}\)
\(=\frac{2sin^2x}{1-sin^2x}=\frac{2sin^2x}{cos^2x}=2tan^2x\)
\(N=\left(\frac{sinx+\frac{sinx}{cosx}}{cosx+1}\right)^2+1=\left(\frac{sinx.cosx+sinx}{cosx\left(cosx+1\right)}\right)^2+1\)
\(=\left(\frac{sinx\left(cosx+1\right)}{cosx\left(cosx+1\right)}\right)^2+1=tan^2x+1=\frac{1}{cos^2x}\)
Câu 1:Đơn giản biểu thức:(-65)-(x+35)+101 ta được kết quả:
A. x B. x - 1 C. 1 - x D. - x
Câu 2:Giá trị của biểu thức a . b^2 với a = 3;b = - 4 bằng
A. - 24 B. 24 C. - 48 D. 48
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 1: C
Câu 2: D
Câu 3: A
Câu 4: B
Đơn giản biểu thức sau: (a + b + c)^3 + ( a - b - c)^3 - 6a(b + c)^2
( a + b + c)3 + (a - b - c)3 - 6a( b+ c)2
= ( a+ b + c + a - b - c)[ (a+b+c)2 + (a+b+c)(a-b-c) + (a-b-c)2 ] - 6a( b+c)2
= 2a [ a2 + b2 + c2 + 2ab+ 2bc+ 2ac + a2 - ( b+ c)2 + a2 + b2 + c2 - 2ab - 2ac + 2bc] - 6a ( b+c)2
= 2a [ 3a2 + 2b2 + 2c2 + 4bc - (b+c)2 - 3(b+c)2}
= 2a ( 3a2 + 2b2 + 2c2 - 4( b+ c)2 + 4bc}
Đặt \(b+c=x\)
Biểu thức đã cho \(=\left(a+x\right)^3+\left(a-x\right)^3-6ax^2=a^3+3a^2x-3ax^2+x^3+a^3-3a^2x+3ax^2-x^3-6ax^2=2a^3\)