Giải các phương trình sau: 3x = 0

Những câu hỏi liên quan
1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
Đúng 1
Bình luận (0)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
Đúng 0
Bình luận (0)
1.
\(a,7x+35=0\\ \Rightarrow7x=-35\\ \Rightarrow x=-5\\ b,ĐKXĐ:x\ne7\\ \dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\\ \Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{8\left(x-7\right)}{x-7}-\dfrac{1}{x-7}=0\\ \Leftrightarrow\dfrac{8-x-8x+56-1}{x-7}=0\\ \Rightarrow-9x+63=0\\ \Leftrightarrow-9x=-63\\ \Leftrightarrow x=7\left(ktm\right)\)
2.đề thiếu
Đúng 0
Bình luận (0)
Giải các phương trình sau:
3x+7=0;
2x(x-2)+2x(5-3x)=0;
`3x+7=0`
`<=>3x=-7`
`<=>x=-7/3`
Vậy `S={-7/3}`
______________________
`2x(x-2)+2x(5-3x)=0`
`<=>2x(x-2+5-3x)=0`
`<=>2x(3-2x)=0`
`@TH1:2x=0<=>x=0`
`@TH2: 3-2x=0<=>2x=3<=>x=3/2`
Vậy `S={0;3/2}`
Đúng 7
Bình luận (2)
3x+7=0
\(\Leftrightarrow3x=-7\Leftrightarrow x=-\dfrac{7}{3}\)
2x(x-2)+2x(5-3x)=0
\(\Leftrightarrow2x\left(x-2+5-3x\right)=0\)
\(\Leftrightarrow2x\left(-2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\-2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-3}{-2}=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 5
Bình luận (1)
3x + 7 = 0
\(\Leftrightarrow\) 3x = -7
\(\Leftrightarrow\) x = -7/3
2x(x - 2) + 2x(5 - 3x) = 0
\(\Leftrightarrow\) 2x(x - 2 + 5 - 3x) = 0
\(\Leftrightarrow\) 2x(-2x + 3) = 0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\-2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (2)
Xem thêm câu trả lời
giải các phương trình sau bằng cách đưa về phương trình tích
3x^3-3x^2-6x=0
3x3 - 3x2- 6x = 0
x ( 3x2 - 3x - 6 ) = 0
x [ 3x2 + 3x - 6x - 6 ] = 0
x [ 3x ( x + 1 ) - 6 ( x + 1 ) ] = 0
x ( 3x - 6 ) ( x + 1 ) = 0
<=> x = 0 hoặc 3x - 6 = 0 hoặc x + 1 = 0
1) x = 0
2) 3x - 6 = 0 <=> x = 2
3) x + 1 = 0 <=> x = -1
Vậy taaph nghiệm của phương trình đã cho S={0 : -1 : 2 }
Đúng 0
Bình luận (0)
\(3x^3-3x^2-6x=0\)
\(3x^3-6x^2+3x^2-6x=0\)
\(3x^2.\left(x-2\right)+3x\left(x-2\right)=0\)
\(\left(3x^2+3x\right)\left(x-2\right)=0\)
\(3x\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow3x=0\) \(\Rightarrow x=0\)hoặc \(\orbr{\begin{cases}x+1=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
Đúng 0
Bình luận (0)
Giải các phương trình sau: 3x - 11 = 0.
3x - 11 = 0 ⇔ 3x = 11 ⇔ 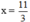 . Vậy phương trình có một nghiệm
. Vậy phương trình có một nghiệm 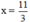 .
.
Đúng 0
Bình luận (0)
Giải các phương trình sau -3x + 18 = 0.
-3x + 18 = 0
⇔ -3x = -18
⇔ x = 6
Phương trình có tập nghiệm S = { 6 }.
Đúng 0
Bình luận (0)
Giải các phương trình sau: 9 x - 3 x - 6 = 0
Giải các phương trình sau: 3x – x + 4 = 0.
3x – x + 4 = 0 ⇔ 2x + 4 = 0 ⇔ 2x = -4 ⇔ x = -2
Vậy phương trình có tập nghiệm S = {-2}.
Đúng 0
Bình luận (0)
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 1
Bình luận (0)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Đúng 1
Bình luận (0)
Giải các phương trình sau: (x + 1)(3x – 3) = 0
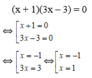
Vậy phương trình đã cho có tập nghiệm là S ={-1; 1}
Đúng 0
Bình luận (0)





















