`a)100x^2-20x+1`

`=(10x-1)^2`

Thay `x=1/10`

`=>100x^2-20x+1=(1-1)^2=0`

`b)49x^2-42x+10`

`=49*4/49-42*2/7+10`

`=4-12+10=2`

`c)25x^2+40x+16y^2`

`=(5x+4y)^2=(2+3)^2=25`

Đáp án: C

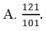
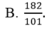
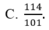
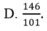
1) Tìm x và y biết

a) (2x+1)² + y² = 0

Ta có : \(\left(2x+1\right)^2\ge0;y^2\ge0\)

\(\Rightarrow\left(2x+1\right)^2+y^2\ge0\)

Để \(\left(2x+1\right)^2+y^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x+1\right)^2=0\\y^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=0\end{matrix}\right.\)

b) x² + 2x + 1 + (y-1)² = 0

\(\Rightarrow\left(x+1\right)^2+\left(y-1\right)^2=0\)

Lập luận tương tự câu a ,ta có :

\(\left(x+1\right)^2+\left(y-1\right)^2\ge0\)

\(\left(x+1\right)^2+\left(y-1\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)^2=0\\\left(y-1\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)

c) x² - 2x + y² + 4y + 5 = 0

\(\Rightarrow\left(x^2-2x+1\right)+\left(y^2+4y+4\right)\)

\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2=0\)

Lập luận tương tự 2 câu trên

\(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

Câu 3: Thay x; y trong số 40xy bởi các chữ số thích hợp để số đó chia hết cho 2; 3; 4 và 5.

A.   x = 4; y = 0             B.x= 4; y = 8                C. x=8; y = 4             D. x =8; y = 0

D nha

x = 2

y = 0

Clikc cho mik nha !!!!!!!!!!!!!!!!!

Muốn chia hết cho cả 2 và 5 thì tận cùng của số đó phải là 0

Muốn chia hết cho 4 thì 2 số tận cùng phải chia hết cho 4 vậy ta có các trường hợp là : 0 ; 2 ; 4 ; 6 ; 8 

Muôns chia hết cho 3 thì tổng các chữ số chia hết cho 3

Vậy b = 2 hoặc 8 

Vậy có tất cả là : 4020 ; 4080

Để 40xy chia hết cho 2 và 5 thì y=0

Ta có số  40x0

Để 40x0 chia hết cho 4 thì \(x\in\left\{0;2;4;6;8\right\}\)

Để 40x0 chia hết cho 3 thì \(x\in\left\{2;8\right\}\)

Vậy x=2 ;y=0

   Hoặc x=8 ;y=0

Vì 40XY chia hết cho 2 và 5 nên 40XY sẽ có tận cùng là 0

=> Y = 0

Ta có 40X0 xhia hết cho 3

Để 40X0 chia hết cho 3 thì 4 + 0 + X + 0 chia hết cho 3

                                               4 + X         chia hết cho 3

=> X = { 2 , 5 , 8 }

Vậy X = { 2 , 5 , 8 } , Y = 0
 

Vì 40xy chia hết cho 2 và 5 => y = 0

Để 40x0 chia hết cho 3 => 4 + 0 + x + 0 chia hết cho 3

                                  => 4 + x chia hết cho 3

=> x = 2 ; 5 ; 8

Vậy ta có số : 4020 ; 4050 ; 4080

Nếu muốn chia hết cho 2 và 5 thì số tận cùng của số đó phải là 0

Muốn chia hết cho 4 thì những số có 2 chữ số tận cùng phải tạo thành số chia hết cho 4 

Vậy ta có các trường hợp là : 2 ; 4 ; 6 ; 8

Nếu muốn chia hết cho 3 thì tổng các chữ số chia hết cho 3

nếu x = 2 thì 4020 chia hết cho 3 thì số này ko chia hết cho 3 ( loại )

Nếu x = 4 thì 4040 chia hết cho 3 thì số này ko chia hết cho 3 ( loại )

nếu x = 6 Thì 4060 chia hết cho 3 thì số này ko chia hết cho 3 ( loại )

Nếu x = 8 thì 4080 thì số này có chia hết cho 3 ( phù hợp )

Vậy số cần tìm là : 4080

Để 40xy chia hết cho 2,5 thì y=0

Để 40xy chia hết cho 4 thì xy =00;40;80

Để 40xy chia hết cho 3 thì 4+0+x+0 chia hết cho 3=>4+x chia hết cho 3 => x =8

=> x=8;y=0

Vì 40xy chia hết cho 2,5 => y=0

=> 40x0 chia hết cho 3,4

40x0 chia hết cho 4 => x=0,2;4;6;8 (1)

40x0 chia hết cho 3 => 4+0+x+0=4+x chia hết cho 3 => x=2;5;8 (2)

Từa (1) và (2) =>x=2;8

Để \(\overline{40xy}\) chia hết cho 2;5 thì \(y=0\)

Thay vào ta được số \(\overline{40x0}\)

Để \(\overline{40x0}\) chia hết cho 3 thì \(4+0+x+0=4+x\) phải chia hết cho 3

\(\Rightarrow x\in\left\{2;5;8\right\}\)

Thay vào ta được các số: \(4020;4050;4080\)

Chúc bạn học tốt!!!

Để \(\overline{40xy}\) chia hết cho 2 và 5 thì y = 0

Thay y = 0 vào ta được \(\overline{40x0}\)

Ta có : một số tự nhiên chia hết cho 3 thì có tổng các chữ số chia hết cho 3

=>Để \(\overline{40x0}\) chia hết cho 3 thì ( 4 + 0 + x + 0) hay ( 4 + x) phải chia hết cho 3

=> \(x\in\left\{2;5;8\right\}\)

=> Ta có số : 4020 ; 4050 ; 4070

Mà số cần tìm pải chia hết cho 7

=> Không có số nào thỏa mãn phải ra.

Vì 40XY chia hết cho 2 và 5 nên 40XY sẽ có tận cùng là 0

=> Y = 0

Ta có 40X0 x chia hết cho 3

Để 40X0 chia hết cho 3 thì 4 + 0 + X + 0 chia hết cho 3

                                          4 + X                 chia hết cho 3

=> X = { 2 , 5 , 8 } Vậy X = { 2 , 5 , 8 } , Y = 0