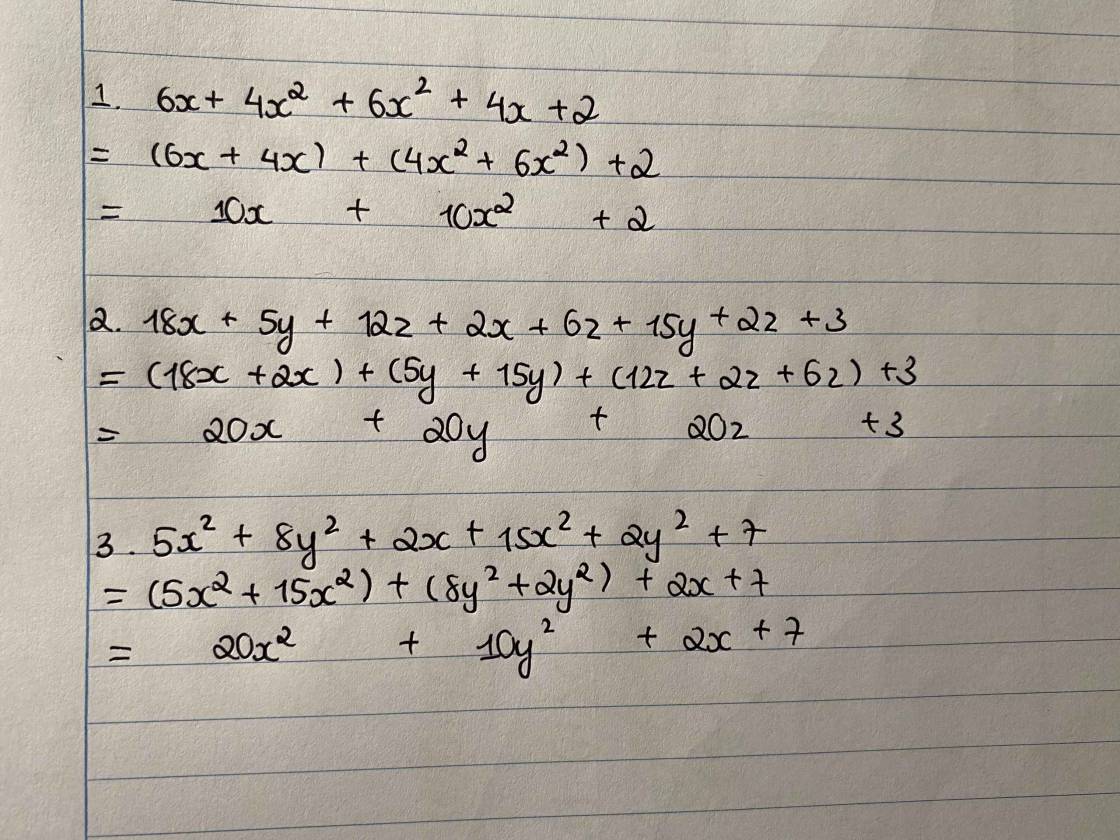thu gọn 15x(x + 2) – 15x2

Những câu hỏi liên quan
Cho đa thức A(x) = x15– 15x14+15x13-15x12+…+15x3-15x2+15x-15. Tính A(14).
Vì x=14 nên x+1=15
Thay 15=x+1 vào A(x) Ta có:
A(x)= x^15-(x+1)x^14+(x+1)x^13-(x+1)x^12+...+(x+1)x^3-(X+1)^2+(x+1)x-15
=x^15-x^15-x^14+x^14+x^13-x^13-...+X^4+x^3-X^3-x^2+x^2-x-15
=x-15
=> A(14)=14-15=-1
Vậy A(14)=-1
k mình nha
Đúng 0
Bình luận (0)
a) Cho đa thức A(x) = x15– 15x14+15x13-15x12+…+15x3-15x2+15x-15.
Tính A(14).
b) Cho đa thức f(x) thỏa mãn điều kiện :
x.f(x-4) = (x-2).f(x).
Chứng minh rằng đa thức f(x) có ít nhất hai nghiệm.
a) Vì x=14 nên x+1=15
Thay 15=x+1 vào A(x) Ta có:
A(x)= x^15-(x+1)x^14+(x+1)x^13-(x+1)x^12+...+(x+1)x^3-(X+1)^2+(x+1)x-15
=x^15-x^15-x^14+x^14+x^13-x^13-...+X^4+x^3-X^3-x^2+x^2-x-15
=x-15
=> A(14)=14-15=-1
Vậy A(14)=-1
b) Với x=10 ta có
0.f(-4)=-2.f(0)
=>0=2.f(0) => f(0)=0
=> Đa thức f(x) có 1 nghiệm là 0 (1)
Với x =2 tao có: 2.f(-2)=0.(f) (2)
Từ (1) và (2)
=> Đa thức này có 2 nghiệm
k mình nha
Đúng 0
Bình luận (0)
Cho hai đa thức P(x)=15x^3+3x+7-x và Q(x)=-15x^3+3x-2+3x-x^2-1
a) thu gọn hai đa thức P(x) và Q(x)
b) Tìm đa thức M(x)=P(x)+Q(x) và N(x)=P(x)-Q(x)
a) Ta có: \(P\left(x\right)=15x^3+3x+7-x\)
\(=15x^3+2x+7\)
Ta có: \(Q\left(x\right)=-15x^3+3x-2+3x-x^2-1\)
\(=-15x^3-x^2+6x-3\)
b) Ta có: M(x)=P(x)+Q(x)
\(=15x^3+2x+7\)\(-15x^3-x^2+6x-3\)
\(=-x^2+8x+4\)
Ta có: N(x)=P(x)-Q(x)
\(=15x^3+2x+7-\left(-15x^3-x^2+6x-3\right)\)
\(=15x^3+2x+7+15x^3+x^2-6x+3\)
\(=30x^3+x^2-4x+10\)
Đúng 0
Bình luận (0)
Thu gọn biểu thức
VD: A= 3x + 5x + 8
A= 8x + 8
1. 6x + 4x2 + 6x2 +4x + 2
2. 18x + 5y + 12z + 2x + 6z + 15y + 2z + 3
3. 5x2 + 8y2 + 2x + 15x2 + 2y2 + 7
a) Cho đa thức A(x) = x15– 15x14+15x13-15x12+…+15x3-15x2+15x-15. Tính A(14).
b) Cho đa thức f(x) thỏa mãn điều kiện : x.f(x-4) = (x-2).f(x). Chứng minh rằng đa thức f(x) có ít nhất hai nghiệm.
HELP ME!
Pn ơi cho mk hỏi tất cả "x" đều là ẩn phải hông?
Đúng 0
Bình luận (0)
Cho biểu thức :
A
15
x
-
11
x
+
2
x
-
3
+
3
x
-
2
1
-
x
-
3
x
+...
Đọc tiếp
Cho biểu thức :
A = 15 x - 11 x + 2 x - 3 + 3 x - 2 1 - x - 3 x + 3 x ≥ 0 ; x ≠ 1
a) Thu gọn biểu thức A.
x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
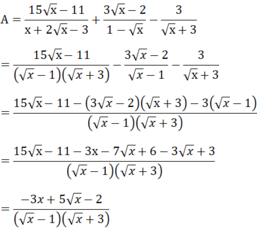
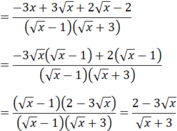
Đúng 0
Bình luận (0)
cho hai đa thức
P(x) = 15x3 - 4x2 - 5x + 1010 - 2x2 và Q(x) = 7x - 15x3 - x2 - 1000 + 3x2 - 2x - 9
thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến
bài 2 : thu gọn đa thức
a .(2a - b) . (b+ 4a) + 2a . (b-3a)
b . (3a - 2b) . (2a-3b) - 6a x (a-b)
c , 5b . (2x - b) - (8b-x) . (2x - b)
d , 2x . (a + 15x) + (x - 6a) . (5a + 2x)
a) \(\left(2a-b\right)\left(b+4a\right)+2a\left(b-3a\right)\)
\(=2ab+8a^2-b^2-4ab+2ab-6a^2\)
\(=\left(2ab+2ab-4ab\right)+\left(8a^2-6a^2\right)-b^2\)
\(=2a^2-b^2\)
b) \(\left(3a-2b\right).\left(2a-3b\right)-6a\left(a-b\right)\)
\(=6a^2-9ab-4ab+6b^2-6a^2+6ab\)
\(=\left(6a^2-6a^2\right)-\left(9ab+4ab-6ab\right)+6b^2\)
\(=-7ab+b^2\)
c) \(5b\left(2x-b\right)-\left(8b-x\right)\left(2x-b\right)\)
\(=10bx-5b^2-\left(16bx-8b^2-2x^2+bx\right)\)
\(=10bx-5b^2-16bx+8b^2+2x^2-bx\)
\(=\left(10bx-16bx-bx\right)-\left(5b^2-8b^2\right)+2x^2\)
\(=-7bx+3b^2+2x^2\)
d) \(2x\left(a+15x\right)+\left(x-6a\right)\left(5a+2x\right)\)
\(=2ax+30x^2+5ax+2x^2-30a^2-12ax\)
\(=\left(2ax+5ax-12ax\right)+\left(30x^2+2x^2\right)-30a^2\)
\(=-5ax+32x^2-30a^2\)
Đúng 2
Bình luận (0)
a: =2ab+8a^2-b^2-4ab+2ab-6a^2
=2a^2-b^2
b: =6a^2-9ab-4ab+6b^2-6a^2+6ab
=-7ab+6b^2
c: =10bx-5b^2-16bx+8b^2+2x^2-xb
=3b^2+2x^2-7xb
d: =2xa+30x^2+5ax+2x^2-30a^2-12ax
=32x^2-30a^2-5ax
Đúng 0
Bình luận (0)
Thu gọn:
\(\text{
a/(x+2)^3-(x-2)^3}\)
b/\(x^3+15x^2+75x+125\)
c/\(x^3-12x^2+48x-64\)
a/ \(x^3+6x^2+12x+8-\left(x^3-6x^2+12x-8\right)=12x^2+16\)
b/ \(=\left(x+5\right)^3\)
c/ \(=\left(x-4\right)^3\)
Đúng 0
Bình luận (0)
rút gọn :15x2-15x8 phần 3+42
15 x 2 - 15 x 8
3 + 42
15 x ( 2 - 8 )
45
= -6 /3
= -2
Đúng 0
Bình luận (0)