Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 c m 2
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ⏜ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 cm 2
Đáp án B.
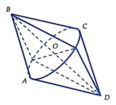
Do A B C ⏜ = 60 ° đều ⇒ A C = 5 c m cm
Do đó diện tích của hình thu được: S = 2 π . AC 2 . BA = 25 π cm 2 cm2
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 0 . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A . S = 25 π 3 3 c m 2
B . S = 25 π c m 2
C . S = 25 π 3 4 c m 2
D . S = 25 π 3 c m 2
Đáp án B.
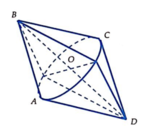
Do ![]() => AC= 5cm
=> AC= 5cm
Do đó diện tích của hình thu được:
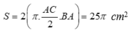
Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a = 5 ; góc BCD = 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và ( SAB ).
A. 450 . B. 300 . C. 600 . D. arctan \(\dfrac{\sqrt{7}}{\sqrt{5}}\)
help me
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 ° cạnh bên SA = a 2 và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90 °
B. 30 °
C. 45 °
D. 60 °
Chọn B.
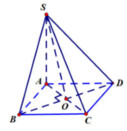
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO ⊥ (SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
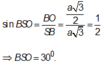
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Cho hình thoi ABCD có cạnh là 5cm, đường cao là 2,5cm và A>B . Số đo các góc của hình thoi là
MN giúp mình với
Cho hình chóp SABCD. ABCD là hình thoi tâm Ở cạnh a. Góc BAD=60°. SO vuông góc với (ABCD). Góc giữa SC và đáy bằng 60°. Tính khoảng cách a)O đến (SBC) b)A đến (SBC) c)AD đến (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc B A D ⏜ có số đo bằng 60 ° . Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng 60 ° . Tính khoảng cách từ B đến mặt phẳng (SCD) .
A. 3 a 17 14
B. 3 a 7 14
C. 3 a 17 4
D. 3 7 4
Đáp án B
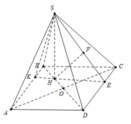
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14
cho hình thoi ABCD có góc B = 60 độ. trên tia đối của CB lấy điểm K sao cho CB = CK.
a) Chứng Minh ABKD là hình gì? vì sao
b) Chứng minh BD vuông góc với DK
c) gọi H ls trọng tâm của ▲ ABC. tính diện tích AHCD, biết cạnh của hình thoi= 5cm
GiÚP MIK VS MIK CẦN GẤP!! THANKS Ạ!!!
bạn tự vẽ hình theo giả thiết nha
a) xét hình thoi ABCD có:
góc B = góc C(t/c hình thoi)
góc A=góc C(t/c hình thoi)
mà góc B = 60 độ(gt)
=>góc C=60 độ
góc A+góc B+góc C+góc D=360 (độ)
thay góc B và góc C=60 độ(cmt)
=>góc A+60 (độ)+góc C+60(độ)=360(độ)
góc A+ góc C= 240(độ)
mà góc A=góc C(cmt)
=>2góc A= 240/2=120(độ)
Xét tứ giác ABKD có
góc BCD+góc DCK=180(độ)(kề bù)
=>góc DCK=180-góc BCD
góc BCD=120 độ (cmt)
=>góc DCK=60 độxét tam CDKBC=CK(gt)mà BC=CD(t/c hình thoi)=>CK=CD(t/c bắc cầu)=>tam CDK là tam cânmà tam cân có một góc=60 độ thì tam CDK là tam đều =>góc K= 60 độ=>góc B= góc C(=60 độ)(1)mà trong hình thoi ABCD có BC//AC(t/c hình thoi)mà điểm K nằm trên tia đốiBC=>BC và CK nằm trên một đường thẳng=>AD//BK=>ADKB là hình thang(dấu hiệu nhận biết hình thang(2)từ (1)(2)=>ABKD là hình thang cân (dấu hiệu nhận biết hình thang cân)b) xét hình thoi ABCD kẻ đường thẳng BC =>BC là đường chéo hình thoi ABCD=>góc ADB=góc BDC(t/c đường chóe hình thoi)=>góc BDC=gócADC/2=30 độgóc BDC +góc CDK= góc BDK=>30(độ)+60(độ)=90(độ)do BDC =30(độ)(cmt)góc CDK=60 độ(cmt)=>góc D = 90 độ=>BD vuông góc DKbạn xem thử có thiếu dữ kiện ở câu c không nha