Cho tam giác MNP vuông tại M. Khi đó cos M N P ^ bằng:
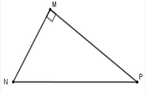
A. M N N P
B. M P N P
C. M N M P
D. M P M N
Cho tam giác MNP vuông tại M. Khi đó cos M N P ^ bằng
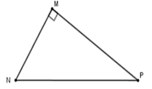
A. M N N P
B. M P N P
C. M N M P
D. M P M N
Tam giác MNP có MN = NP và góc M bằng 45ᵒ, khi đó kết luận nào sau đây là đúng nhất?
Tam giác MNP vuông tại M
Tam giác MNP đều
Tam giác MNP cân tại N
Tam giác MNP vuông cân tại N
Cho tam giác MNP vuông tại M. Khi đó tan M N P ^ bằng:
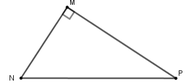
A. M N N P
B. M P N P
C. M N M P
D. M P M N
Ta có: tan M N P ^ = M P M N
Đáp án cần chọn là: D
Cho tam giác MNP vuông tại M có MN = 6 cm ,MP=8cm khi đó NP bằng:
a 🔼MNP vuông tại M b 🔼MNP vuông tại P
c 🔼MNP vuông tại N d 🔼MNP cân tại P
Cho tam giác MNP vuông tại M. Khi đó cos M N P ^ bằng
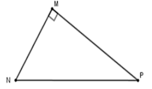
A. M N N P
B. M P N P
C. M N M P
D. M P M N
cho đường tròn tâm (O;R) ngoại tiếp tam giác MNP vuông cân tại M khi đó MN bằng ?
cho tam giác MNP vuông tại M có MN = 6 cm,MP=8 cm .khi đó NP bằng
A. 100cm B.10cm C.14cm D.48cm
Cho tam giác MNP vuông cân tại M có NP= căn bậc 2 của 32 cm, khi đó độ dài cạnh MN bằng:
Ta có
\(NP=\sqrt{32}=4\sqrt{2}cm\)
Mà \(\Delta MNP\) vuông cân
\(\Rightarrow MN=NP\)
Áp dụng định lí Pytago ta có
\(NP^2=NM^2+MP^2\\ mà.MN=NP\\ \Rightarrow MN=\dfrac{NP}{2}=.....\)
Cho tam giác ABC vuông tại A có góc B bằng 30° và tam giác MNP vuông tại góc M có góc P bằng 60°. Chứng minh tam giác ABC đồng dạng với tam giác MNP.
Ta có: <A+<B+<C=180
90+30+<C=180
<c=180-30-90=60
Xét ▲ABC và ▲MNP ta có:
<A=<M=90
<C=<P(=60)
Do đó ▲ABC đồng dạng ▲MNP(g-g)