Cho hàm số y = a x 2 với a ≠ 0. Kết luận nào sau đây là đúng
A. Hàm số nghịch biến khi a > 0 và x > 0
B. Hàm số nghịch biến khi a < 0 và x < 0
C. Hàm số nghịch biến khi a > 0 và x < 0
D. Hàm số nghịch biến khi a > 0 và x = 0
Cho hàm số y = ( \(m^2\) + 2021 ) \(x^2\). Kết luận nào sau đây đúng?
A. Hàm số nghịch biến khi x <0
B. Hàm số đồng biến khi x <0
C. Hàm số nghịch biến khi x > 0
D. Hàm số đồng biến khi x \(\le\) 0
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
Cho hàm số y = -3 x 2 . Khẳng định nào sau đây là đúng?
A) Khi 0 < x < 15, hàm số đồng biến
B) Khi -1 < x < 1, hàm số đồng biến
C) Khi -15 < x < 0, hàm số đồng biến
D) Khi -15 < x < 1, hàm số đồng biến
Cho hàm số: y = -3 x 2 . Ta có: a = -3 < 0 nên hàm số đồng biến khi x < 0.
Chọn C) Khi -15 < x < 0, hàm số đồng biến.
Cho hàm số y = a x 2 với a ≠ 0. Kết luận nào sau đây là đúng
A. Hàm số đồng biến khi a > 0 và x < 0
B. Hàm số đồng biến khi a > 0 và x > 0
C. Hàm số đồng biến khi a > 0 và x < 0
D. Hàm số đồng biến khi a < 0 và x = 0
Cho hàm số y = ax2(a ≠ 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Đáp án cần chọn là: B
Cho hàm số y = a x 2 với a ≠ 0. Kết luận nào sau đây là đúng:
A. Hàm số nghịch biến khi a > 0 và x > 0
B. Hàm số nghịch biến khi a < 0 và x < 0
C. Hàm số nghịch biến khi a > 0 và x < 0
D. Hàm số nghịch biến khi a > 0 và x = 0
Đáp án C
Cho hàm số
• Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
• Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Hãy vẽ đồ thị của các hàm số y = 2 x 2 , y = - 2 x 2 . Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số y = a x 2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số y = a x 2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Vẽ hình:
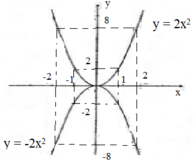
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.