Đáp án D

Cách giải:

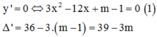
+  => Hàm số đồng biến trên 

+  Phương trình (1) có 2 nghiệm phân biệt 

Theo đinh lí Viet ta có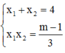

Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì

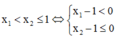
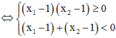
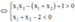
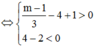 ( vô lí )

Vậy m ≥ 13

Mà 

Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006

Đáp án A.

Ta có y ' = − 3 x 2 − 6 x + 4 m =>Hàm số nghịch biến trên  − ∞ ; 0

⇔ y ' ≤ 0 ∀ x ∈ − ∞ ; 0 ⇔ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0

Bảng biến thiên:

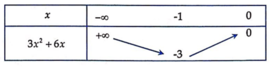
  ⇒ 3 x 2 + 6 x ≥ − 3 ∀ x ∈ − ∞ ; 0 ⇒ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0

⇔ 4 m ≤ − 3 ⇔ m ≤ − 3 4 ⇒ m ∈ − 2018 ; − 3 4 m ∈ ℤ

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)

Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)

\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)

Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2

m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}

Vậy có 2016 giá trị nguyên của m cần tìm.

Chọn D.

3.

\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)

Hàm nghịch biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)

\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)

4.

\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)

Hàm đồng biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)

\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Đáp án D.