Đáp án D
Cách giải:
![]()
![]()
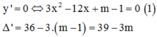
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 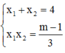
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
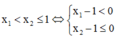
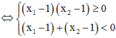
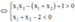
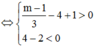 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
Đáp án D
Cách giải:
![]()
![]()
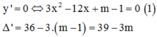
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 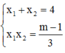
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
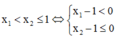
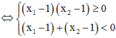
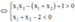
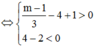 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
Số giá trị nguyên dương của m để hàm số y = 1 3 x 3 - 3 x 2 + ( m - 2017 ) x + 2018 nghịch biến trên khoảng (0;2) là
A. 2015.
B. 2017.
C. 2016.
C. 2016.
Có bao nhiêu giá trị nguyên của m lớn hơn -2018 để hàm số y = − x 3 − 3 x 2 + 4 m x − 2018 nghịch biến trên ( − ∞ ; 0 ) ?
A. 2017
B. 2018.
C. 2019
D. Vô số
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = 1 3 x 3 − 1 2 m x 2 + x + 2018 đồng biến trên R?
A. 5
B. 3
C. 4
D. 2
Có bao nhiêu giá trị nguyên dương của m, không lớn hơn 2018, sao cho giá trị nhỏ nhất của hàm số y = m x 3 3 − x 2 − m − 2019 x + 1 trên đoạn [6;9] luôn lớn hơn 69069 ?
A. 1069.
B. 1696.
C. 1801.
D. 1155.
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số y = x - 2 x - m nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
A. 2015
B. 2016
C. 2017
D. 2014
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = x 2 2 - m x + ln ( x - 1 ) đồng biến trên khoảng ( 1 ; + ∞ ) ?
A. 3
B. 4.
C. 2.
D. 1.
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = x 2 2 – m x + l n ( x - 1 ) đồng biến trên khoảng (1;+∞) ?
A. 4
B. 1
C. 3
D. 2
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 4 ( x 2 + m x + 9 ) với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(3 - x) đồng biến trên khoảng 3 ; + ∞
A. 5
B. 6
C. 7
D. Vô số
Cho hàm số bậc ba y = f x có đồ thị như hình vẽ bên. Có bao nhiêu số tự nhiên m ≤ 2018 để hàm số y = f m - x + m - 1 x đồng biến trên khoảng (-1;1)
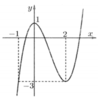
A. 2
B. 3
C. 1
D. 2018