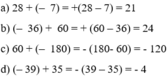giúp mik vs 

Lời giải:

$\overrightarrow{AB}\parallel \overrightarrow{C'D'}$ và $|\overrightarrow{AB}|=|\overrightarrow{C'D'}|=a$ nên:

$\overrightarrow{AB}.\overrightarrow{C'D'}=a^2$

Do tất cả các cạnh bằng a nên các mặt bên đều là hình thoi.

Mà \(\widehat{BAA'}=\widehat{BAD}=\widehat{DAA'}=60^0\Rightarrow A'B=A'D=AA'=BD=a\)

\(\Rightarrow\) Hình chiếu vuông góc H của A' lên (ABCD) là tâm tam giác đều ABD 

\(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AC=a\sqrt{3}\)

\(cos\widehat{A'AC}=\dfrac{AH}{AA'}=\dfrac{\sqrt{3}}{3}\Rightarrow cos\widehat{ACC'}=-\dfrac{\sqrt{3}}{3}\)

Áp dụng định lý hàm cos cho tam giác ACC':

\(AC'=\sqrt{AC^2+C'C^2-2AC.C'C.cos\widehat{ACC'}}=a\sqrt{6}\)

a) trên nữa mp bờ chứa tia ox ta có  xot<xoy(30<60)

      ⇒ot nằm giữa 2 tia còn lại

     ⇒ xot + toy = xoy

      30 độ + toy = 60 độ

                    toy = 60 độ - 30 độ = 30 độ 

b) vì ox' và ox 2 là tia đối 

    ⇒ tia x'oy  và xoy là 2 góc kề bù 

  ⇒ x'oy + xoy = 180 

      x'oy + 60 độ = 180 độ

     x'oy                = 180 độ - 60 độ = 120 độ 

 vì oy và oy' là 2 tia đối nhau

  ⇒ x'oy và x'oy' là 2 góc kề bù

    ⇒ x'oy + x'oy' = 180 độ

     120 độ + x'oy' = 180 độ

                  x'oy'    = 180 độ = 120 độ = 60 độ 

vậy x'oy' = 60 độ

Ta có: \(\widehat{xOy}=\widehat{x'Oy'}\)(Hai góc đối đỉnh)

mà \(\widehat{xOy}=60^0\)

nên \(\widehat{x'Oy'}=60^0\)

Vậy: \(\widehat{x'Oy'}=60^0\)

https://sites.google.com/site/dangcapcuatoanhoc/toan-6/bai-15-tia-phan-giac-cua-goc?tmpl=%2Fsystem%2Fapp%2Ftemplates%2Fprint%2F&showPrintDialog=1