a: Xét ΔABC có \(AB^2=AC^2+BC^2\)

nên ΔABC vuông tại C

Nếu AB + AC = 14; AB - AC = 2 thì

\(\Rightarrow\left\{{}\begin{matrix}2AB=14+2=16\\AC=14-AB\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}AB=16:2=8\\AC=14-8=6\end{matrix}\right.\) 

Áp dụng định lý Pitago

\(BC^2=AB^2+AC^2\\ =\sqrt{6^2+8^2}=10\)

3.Cho tam giác ABC vuông tại A có AB= 14cm, BC= 50cm. Gọi h là trung điểm AC. Đường vuông góc được vẽ từ H của AC cắt đường phân giác góc B ở K, và cắt BC tại M. Từ H hạ HD vuông góc BC (H thuộc BC).

a) tính HC.

b) CM: tam giác BKC vuông.

c) tính BK.

d) CM: DB^2 – DC^2= AB^2

a) ΔAHB∼ΔCAB(g-g)

ΔAHC∼ΔBAC(g-g)

ΔAHB∼ΔCAH(g-g)

b) Xét ΔABH có 

BD là đường phân giác ứng với cạnh AH(gt)

nên \(\dfrac{AD}{DH}=\dfrac{AB}{BH}\)(Tính chất đường phân giác của tam giác)(1)

Xét ΔABC có 

BE là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{EC}{AE}=\dfrac{BC}{BA}\)(Tính chất đường phân giác của tam giác)(2)

Ta có: ΔABC\(\sim\)ΔHBA(cmt)

nên \(\dfrac{BC}{BA}=\dfrac{BA}{BH}\)(Các cặp cạnh tương ứng tỉ lệ)(3)

Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DH}=\dfrac{EC}{AE}\)

hay \(AD\cdot AE=EC\cdot DH\)(đpcm)

Câu a dài mà cơ bản quá, mình làm câu b thôi nhé.

b) Ở câu a ta chứng minh được ∆ABH~∆CBA:

=> \(\dfrac{AB}{BH}=\dfrac{BC}{AB}\)

Mà BD là phân giác góc HBA

=> \(\dfrac{BH}{AB}=\dfrac{DH}{AD}\)

BE là phân giác góc CBA

=> \(\dfrac{AB}{BC}=\dfrac{AE}{EC}\)

Mà \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)

=> \(\dfrac{AE}{EC}=\dfrac{DH}{AD}\Leftrightarrow AD.AE=DH.EC\)

=> Đpcm

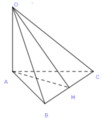
Gọi H là chân đường cao kẻ từ A xuống BC trong tam giác ABC.

+ Ta có: A H ⊥ B C O A ⊥ B C ⇒ B C ⊥ O A H ⇒ O H ⊥ B C     ⇒  d(O; BC) = OH

+ Nửa chu vi tam giác ABC: p = 14 + 16 + 10 2 = 20

S A B C = 20 20 − 14 20 − 16 20 − 10 = 40 3 (theo công thức Hê-rông)

Lại có S A B C = 1/2AH.BC  ⇒ AH =  2 S A B C B C = 80 3 10 = 8 3 .

+ Tam giác OAH vuông tại A (OA ⊥ AH)

⇒  OH =  O A 2 + A H 2 = 8 2 + 8 3 2 = 16.

Vậy d(O; BC) = OH = 16.

Đáp án B