Cho hình bình hành ABCD có góc a = 3 góc B . Tính số đo các góc của hình bình hành

Những câu hỏi liên quan
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD, AB= 10cm, AD= 6cm, góc A > góc B. Tính số đo các góc của hình bình hành ABCD.
mình dốt hình lắm chỉ biết số học thôi
CHÚC BẠN HỌC GIỎI
TK MÌNH NHÉ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD là hình bình hành số đo góc a bằng 120 độ tính số đo góc còn lại của hình bình hành
Vì ABCD là hbh nên \(\widehat{A}=\widehat{C}=120^0\) và AB//CD
Do đó \(\widehat{B}=\widehat{D}=180^0-\widehat{A}=60^0\) (trong cùng phía)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc A = 3 góc D Số đo góc C hình của hình thành là
Ta có: \(\widehat{A}+\widehat{D}=180^o\Rightarrow4\widehat{D}=180^o\Rightarrow\widehat{D}=45^o\)
Ta có:\(\widehat{C}+\widehat{D}=180^o\Rightarrow\widehat{C}=135^o\)
Đúng 3
Bình luận (0)
Cho hình bình hành ABCD,góc ACD=1/2 gocsD .gọi M là trung điểm của AB hai tia CM và DA cắt nhau tại E . a,Cm:tứ giác AEBC là hình bình hành b,Để hình bình hành AEBC là hình chữ Nhật thì số đo các góc của hình bình hành ABCD là bao nhiêu
a: Xét ΔMEA và ΔMCB có
góc EMA=góc CMB
MA=MB
góc MEA=góc MCB
=>ΔMEA=ΔMCB
=>ME=MC
=>M là trung điểm của CE
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
=>AEBC là hbh
b: Để AEBC là hình chữ nhật thì góc EAC=90 độ
=>góc DAC=90 độ
=>góc ACD+góc D=90 độ
mà góc ACD=1/2*góc D
nên góc D=2/3*90=60 độ
=>góc B=60 độ
góc BAD=góc BCD=180-60=120 độ
Đúng 1
Bình luận (0)
tính số đo các góc của hình bình hành ABCD biết Â+góc B+ góc C=230 độ
Xét h.b.h ABCD
có: ^A + ^B + ^C + ^D = 360 độ
=> ^D = 130
mà ^A + ^D = 180 độ ( trong cùng phía)
=> ^A = 50 độ
mà ^A = ^C = 50 độ ( ABCD là h.b.h; ^A và ^C là 2 góc đối)
=> ^C = 50 độ
^D = ^B = 130 độ ( 2 góc đối)
=> ^B = 130 độ
Đúng 0
Bình luận (0)
xét hình bình hành ABCD,ta có:
góc A+ góc B +góc C +góc D=360o
mà góc A+ góc B +góc C=230o
=>góc D=360-230=130o
mà góc A+góc D=180o
=>góc A=180-130=50o
do góc A và góc C là hai góc đối =>góc A+góc C=180o=>góc C=180o-50o=130o
do góc B và góc D là hai góc đối =>góc B+góc D=180o=>góc B=180o-130o=50o
vậy góc A=50o
góc B=50o
góc C=150o
góc D=150o
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc A = 110 độ. Ở phía ngoài của hình bình hành vẽ các tam giác đều ABE và ADF.
a) TÍnh số đo góc EAF
b) Chứng minh tam giác EAF = tam giác CDF
c) Chứng minh tam giác EFC là tam giác đều
Bạn tự vẽ hình nhé!
Giải
a) Ta có:
\(\widehat{EAF}+\widehat{EAB}+\widehat{BAD}+\widehat{DAF}=360^0\)
\(\Rightarrow\widehat{EAF}+60^0+60^0+110^0=360^0\)
\(\Rightarrow\widehat{EAF}=130^o\)
b) Vì ABCD là hình bình hành nên:
\(\widehat{BAD}+\widehat{ADC}=180^o\)
\(110^o+\widehat{ADC}=180^o\)
\(\Rightarrow\widehat{ADC}=70^o\)
\(\Rightarrow\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=70^o+60^o=130^o\)
Xét \(\Delta\)EAF và \(\Delta\)CDF có:\(\hept{\begin{cases}AE=DC\left(=AB\right)\\AF=DF\\\widehat{EAF}=\widehat{CDF}=130^o\end{cases}\Rightarrow\Delta EAF=\Delta CDF\left(cgc\right)}\)
c) Ta có: \(\Delta EAF=\Delta CDF\left(cmt\right)\Rightarrow EF=CF\)
Tương tự cũng có: \(\Delta CDF=\Delta EBC\left(cgc\right)\Rightarrow CF=EC\)
\(\Rightarrow\Delta\)EFC là tam giác đều (đpcm)
Quan sát hình bình hành ở hình 4.12a.
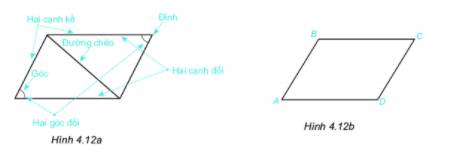
1. Dùng thước thẳng đo và so sánh độ dài các cạnh đổi của hình bình hành ABCD (1.4.12b).
2. Các góc đối của hình bình hành ABCD có bằng nhau không?
3. Các cạnh đối của hình bình hành ABCD có song song với nhau không?
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
Đúng 1
Bình luận (0)
Hình bình hành ABCD có góc B = 1/3 góc A. Khi đó số đo góc C là bao nhiu???
Hình bạn tụ vẽ nhé =))
Theo bài ra , ta có :
\(3\widehat{B}=\widehat{A}\)
mà \(\widehat{A}+\widehat{D}=180^O\)( vì hai góc này ở vị trí trong cùng phía )
=) \(3\widehat{B}=\widehat{D}=\frac{180^O}{3}=60^O\)
mà \(\widehat{B}+\widehat{C}=180^O\) ( vì hai góc này ở vị trí trong cùng phía )
nên \(\widehat{C}=180^O-60^O=120^O\)
Vậy ta có đpcm
Đúng 0
Bình luận (0)






















