Cho hàm số y = x 2 − 2 x − 2 có đồ thị (P), và đường thẳng (d) có phương trình y = x + m . Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho O A 2 + O B 2 đạt giá trị nhỏ nhất
A. m = − 5 2
B. m = 5 2
C. m = 1
D. m = 2
Cho hàm số \(y=\dfrac{1}{2}x^2\) có đồ thị thì (P) và đường thẳng (d) có phương trình: \(y=x+1\)
a, Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ Oxy
b, Tìm tọa độ giao điểm của 2 hàm số trên.
cho hàm số y=\(\dfrac{-x^2}{2}\) có đồ thị (P) và đường thẳng(d):y=-5x+2
a) Gọi M là điểm thuộc (P) có hoành độ x=-3. Viết phương trình đường thẳng OM
b) Đường thẳng CE căt đồ thị (P) tại hai điểm có hoành độ là -1 và 2.viết pt đường thẳng CE
Lời giải:
a) $y_M=\frac{-x_M^2}{2}=\frac{-(-3)^2}{2}=\frac{-9}{2}$
Đường thẳng $OM$ có dạng: $y=ax$
$\Rightarrow y_M=ax_M\Leftrightarrow \frac{-9}{2}=a.(-3)$
$\Rightarrow a=\frac{3}{2}$
Vậy ĐT $OM$ là: $y=\frac{3}{2}x$
b) Gọi PTĐT $CE$ có dạng $y=ax+b$
PT hoành độ giao điểm giữa $(P)$ và $CE$ là:
$\frac{-x^2}{2}-ax-b=0$
$\Leftrightarrow x^2+2ax+2b=0(*)$
$(P)$ và $CE$ cắt nhau tại 2 điểm có hoành độ $-1;2$ nghĩa là PT $(*)$ nhân $x=-1$ và $x=2$ là nghiệm
\(\Rightarrow \left\{\begin{matrix} 1-2a+2b=0\\ 4+4a+2b=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{-1}{2}\\ b=-1\end{matrix}\right.\)
Vậy PTĐT $CE$ có dạng $y=-\frac{1}{2}x-1$
Cho hàm số \(y=\frac{1}{2}x^2\) có đồ thị (P).
a) Vẽ đồ thị (P) của hàm số.
b) Tìm tọa độ giao điểm của đồ thị (P) và đường thẳng d có phương trình y = x + 4.
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x^2-x-4=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-8=0\\y=x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+2\right)=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;8\right);\left(-2;2\right)\right\}\)
Bài 8. Cho hàm số y=ax+b
a. Tìm a, b biết đường thẳng (d) đi qua A(2; -2) và song song với đường thẳng (d’) có phương trình y = 1 /2 x+1
b. Vẽ đồ thị hàm số với a, b tìm được.
Bài 8. Cho hàm số y=ax+b a. Tìm a, b biết đường thẳng (d) đi qua A(2; -2) và song song với đường thẳng (d’) có phương trình y = 1 /2 x+1
b. Vẽ đồ thị hàm số với a, b tìm được.
cho hàm số \(y=x^2-2x-2\) có đồ thị là parabol (P) và đường thẳng d có phương trình y = x - m. giá trị của m để đường thẳng d cắt (P) tại 2 điểm phân biệt A, B sao cho \(OA^2+OB^2\) đạt giá trị nhỏ nhất
Cho hàm số 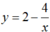 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
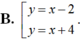
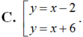
D. Không tồn tại.
Chọn C.
Đạo hàm: 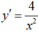
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình 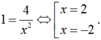
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
Cho hàm số y=ax+b
a. Tìm a, b biết đường thẳng (d) đi qua A(2; -2) và song song với đường thẳng (d’) có phương trình y = 1 /2 x+1
b. Vẽ đồ thị hàm số với a, b tìm được.
giúp/mình/mình/đang/cần/gấp
a) (d) đi qua \(A\left(2;-2\right)\Rightarrow-2=2a+b\)
Vì \((d)\parallel (d')\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
\(\Rightarrow-2=1+b\Rightarrow b=-3\Rightarrow y=\dfrac{1}{2}x-3\)
b) Có a,b rồi thì bạn tự vẽ nha
Cho hàm số \(y = -{ 1} /2 x^2\) có đồ thị ( P) và đường thẳng ( d ) y = 3 - 4x. lập phương trình đường thẳng ( d' ) song song với ( d ) và cắt ( P ) tại điểm M có hoành độ bằng 2
1) Vẽ đồ thị (P) của hàm số : y = x2
2) Tìm tọa độ giao điểm của đồ thị (P) và đường thẳng (d) có phương trình y = 2x +3
1/ Cái vẽ bạn phải tự làm thôi.
2/ Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2x+3\)
\(\Leftrightarrow x^2-2x-3=0\)
( a = 1; b = -2; c = -3 )
Ta có: a - b + c = 1 + 2 - 3 = 0
Phương trình có 2 nghiệm: \(x_1=-1;x_2=-\frac{c}{a}=-3\)
* Thay \(x_1=-1\)vào: \(y=x^2\Leftrightarrow y=\left(-1\right)^2=1\)
* Thay \(x_2=-3\)vào: \(y=x^2\Leftrightarrow y=\left(-3\right)^2=9\)
Vậ tọa độ giao điểm của (P) và (d) là: (-1;1) và (-3;9)