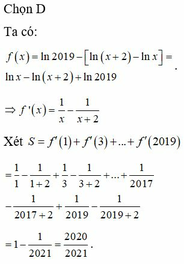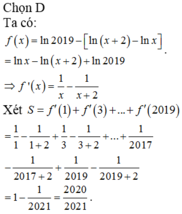tính tổng S=\(2C^0_{2019}+3C^1_{2019}+4C^2_{2019}+.....+2021C^{2019}_{2019}\)

Những câu hỏi liên quan
Rút gọn tổng \(S=C\overset{1}{2019}-2C\overset{2}{2019}+...-2018C\overset{2018}{2019}+2019C\overset{2019}{2019}\) bằng:
A. 2019
B.1
C. -2019
D. 0
Rút gọn tổng: \(S=-C\overset{1}{2019}+1.2C\overset{2}{2019}-2.3C\overset{3}{2019}+...+2017.2018C\overset{2018}{2019}-2018.2019C\overset{2019}{2019}\) bằng:
A. 1
B.. 2019
C. 0
D. -2019
Tính tổng sau: \(C^1_{2021}+C^3_{2021}+C^5_{2021}+...+C^{2017}_{2021}+C^{2019}_{2021}.\)
Xét khai triển:
\(2^{2021}=\left(1+1\right)^{2021}=C_{2021}^0+C_{2021}^1+...+C_{2021}^{2020}+C_{2021}^{2021}\) (1)
\(0=\left(1-1\right)^{2021}=C_{2021}^0-C_{2021}^1+C_{2021}^2+...+C_{2021}^{2020}-C_{2021}^{2021}\) (2)
Trừ vế cho vế (1) và (2):
\(2^{2021}=2.C_{2021}^1+2.C_{2021}^3+...+2C_{2021}^{2021}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}+C_{2021}^{2021}=\dfrac{2^{2021}}{2}=2^{2020}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}+1=2^{2020}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}=2^{2020}-1\)
Đúng 0
Bình luận (0)
cho các số dương a, b, c, d sao cho a/b = c/d. CMR: (2a + 3b/2c + 3d)^2019 = 5a^2019 + 7b^2019/5c^2019+7d^2019)
Tính tổng :
\(\frac{2019}{210}+\frac{2019}{280}+\frac{2019}{360}+\frac{2019}{450}+\frac{2019}{550}\)
\(\frac{2019}{210}+\frac{2019}{280}+\frac{2019}{360}+\frac{2019}{450}+\frac{2019}{550}\)
\(=\frac{673}{70}+\frac{2019}{280}+\frac{673}{120}+\frac{673}{150}+\frac{2019}{550}\)
\(=\left[\frac{673}{70}+\frac{2019}{280}\right]+\frac{673}{120}+\frac{673}{150}+\frac{2019}{550}\)
\(=\left[\frac{2692}{280}+\frac{2019}{280}\right]+\frac{673}{120}+\frac{673}{150}+\frac{2019}{550}\)
\(=\frac{673}{40}+\frac{673}{120}+\frac{673}{150}+\frac{2019}{550}\)
\(=\left[\frac{673}{40}+\frac{673}{120}\right]+\frac{673}{150}+\frac{2019}{550}\)
\(=\left[\frac{2019}{120}+\frac{673}{120}\right]+\frac{673}{150}+\frac{2019}{550}\)
\(=\frac{673}{30}+\frac{673}{150}+\frac{2019}{550}\)
\(=\left[\frac{673}{30}+\frac{673}{150}\right]+\frac{2019}{550}\)
\(=\frac{673}{25}+\frac{2019}{550}=\frac{14806}{550}+\frac{2019}{550}=\frac{16825}{550}=\frac{673}{22}\)
P/S : Các a chị check dùm em ạ
Đúng 0
Bình luận (0)
cho a,b,c thỏa mãn (a+b+c)(ab+bc+ca)=2019, abc =2019. tính P= (b^2c+ 2019)(c^2 a+ 2019)(a^2 c+2019)
Cho \(\frac{a}{b}=\frac{c}{d}cmr:a.\left(\frac{a-b}{c-d}\right)^{2019}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\)
Cho hàm số
f
x
ln
2019
-
ln
x
+
2
x
. Tính tổng
S
f
1
+
f
3
+
...
Đọc tiếp
Cho hàm số f x = ln 2019 - ln x + 2 x . Tính tổng S = f ' 1 + f ' 3 + . . . + f ' 2019 .
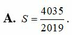
![]()
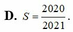
Cho \(\frac{a}{b}=\frac{c}{d}\). Chứng minh: \(\left(\frac{a-b}{c-d}\right)^{^{2019}}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\)
- Nếu \(a=c=0\Rightarrow\left(\frac{a-b}{c-d}\right)^{2019}=\left(\frac{b}{d}\right)^{2019}=\frac{b^{2019}}{d^{2019}}\)
\(\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}=\frac{-b^{2019}}{-d^{2019}}=\frac{b^{2019}}{d^{2019}}\Rightarrow\left(\frac{a-b}{c-d}\right)^{2019}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\)
- Nếu \(a;c\ne0\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{2a^{2019}}{2c^{2019}}=\frac{a^{2019}}{c^{2019}}=\frac{b^{2019}}{d^{2019}}=\left(\frac{a-c}{b-d}\right)^{2019}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\)
Có \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{a^{2019}}{c^{2019}}=\frac{b^{2019}}{d^{2019}}=\frac{\left(a-b\right)^{2019}}{\left(c-d\right)^{2019}}\left(1\right)\)
Có \(\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^{2019}}{c^{2019}}=\frac{b^{2019}}{d^{2019}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a^{2019}}{c^{2019}}=\frac{b^{2019}}{d^{2019}}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\frac{\left(a-b\right)^{2019}}{\left(c-d\right)^{2019}}=\frac{2a^{2019}-b^{2019}}{2c^{2019}-d^{2019}}\)
Cho hàm số
f
(
x
)
ln
2019
-
ln
x
+
2
x
tính tổng
S
f
(
1
)
+
f
(
3
)
+
.
.
.
+
f
(...
Đọc tiếp
Cho hàm số f ( x ) = ln 2019 - ln x + 2 x tính tổng S = f ' ( 1 ) + f ' ( 3 ) + . . . + f ' ( 2019 )
A. 4305 2019
B. 2021
C. 2019 2021
D. 2020 2021