Cho tam giác ABC có \(\widehat{A}=2\widehat{B}\), AB = 11cm, AC = 25 cm. Tính BC

Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat{B}=2.\widehat{C}\), AB=5cm, AC=8cm. Tính BC
Bài 1 : Cho hình thang ABCD (AB//CD), widehat{A}widehat{D}90o , AB11cm , AD 12 cm, Bc 13 cm . Tính ACBài 2 : Cho ΔABC cân tại A. Trên cạnh AB,AC lấy điểm M,N sao cho BM CNa)Tứ giác BMNC là hình gì ? Vì sao ?b)Tính các góc của tứ giác BMNC biết rằng widehat{A} bằng 40o
Đọc tiếp
Bài 1 : Cho hình thang ABCD (AB//CD), \(\widehat{A}\)=\(\widehat{D}\)=90o , AB=11cm , AD= 12 cm, Bc = 13 cm . Tính AC
Bài 2 : Cho ΔABC cân tại A. Trên cạnh AB,AC lấy điểm M,N sao cho BM = CN
a)Tứ giác BMNC là hình gì ? Vì sao ?
b)Tính các góc của tứ giác BMNC biết rằng \(\widehat{A}\) bằng 40o
Bài 2:
a) Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(AM=AN;AB=AC\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét tứ giác BMNC có MN//BC(gt)
nên BMNC là hình thang có hai đáy là MN và BC(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 1
Bình luận (0)
Cho tam giác ABC có \(\widehat{B}=60^o\) . CM: \(AC^2=AB^2+BC^2-AB.BC\)
Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(BA^2+BC^2-AC^2=2\cdot BA\cdot BC\cdot cos60=BA\cdot BC\)
=>AC^2=BA^2+BC^2-BA*BC
Đúng 2
Bình luận (0)
Cho tam giác vuông ABC(A=90) có AB=4cm, BC=5cm.Trên tia AC lấy D sao cho\(\widehat{ABC}=\widehat{ACB}\). Kẻ AE vuông góc với BD
a)Tính AC
b) so sánh: \(\widehat{ABC}=\widehat{ACB}\), AC và AD
c) CM: AE đi qua trung điểm của BC
d) Kẻ đường trung tuyến của BC
e) kẻ đường trung tuyến của BC cảu tam giác ABC cắt AE tại G. tính AG
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
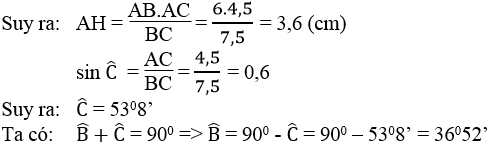 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 2 lần góc B, AB=11cm, AC=25 cm. Tính BC
Mong mọi người giúp đỡ, mai em phải nộp rồi
Cho tam giác ABC có \(\widehat{A}=2\widehat{B}=3\widehat{C}=4\alpha\)CM \(\frac{1}{AB}=\frac{1}{AC}+\frac{1}{BC}\)
Cho tam giác ABC cân tại A với BC=2, M là trung điểm BC. Lấy D, E thuộc AB, AC sao cho\(\widehat{DME}=\widehat{B}\)
a. CM: tích BD. CE không đổi
b. DM là tia phân giác của \(\widehat{BDE}\)
c. Tính chu vi của tam giác AED nếu tam giác ABC là tam giác đều
Hình tự vẽ nhá
Vì tam giác ABC cân tại A nên:
\(\widehat{B}=\widehat{C}\)
Mà \(\widehat{B}=\widehat{DME}\)
Suy ra: \(\widehat{C}=\widehat{DME}\)
Mặt khác: \(\widehat{BME}=\widehat{BMD}+\widehat{DME}=\widehat{MEC}+\widehat{C}\)(góc ngoài của tam giác MEC)
Suy ra: \(\widehat{BMD}=\widehat{MEC}\)
Xét tam giác BMD và tam giác CEM có:
+ \(\widehat{B}=\widehat{C}\)(gt)
+\(\widehat{BMD}=\widehat{MEC}\)(cmt)
Do đó: \(\Delta BMD~\Delta CEM\)(g.g)
Suy ra: \(\frac{BM}{CE}=\frac{BD}{CM}\Leftrightarrow BM\cdot CM=CE\cdot BD\)
Vì BM,CM không đổi (vì BM=CM) nên BM.CM không đổi
Vậy BD.CE không đổi
Đúng 0
Bình luận (0)
ý c nhé, a và b dễ tự làm nhé:
https://vn.answers.yahoo.com/question/index?qid=20110323013140AAJ5GpF
Đúng 0
Bình luận (0)
















