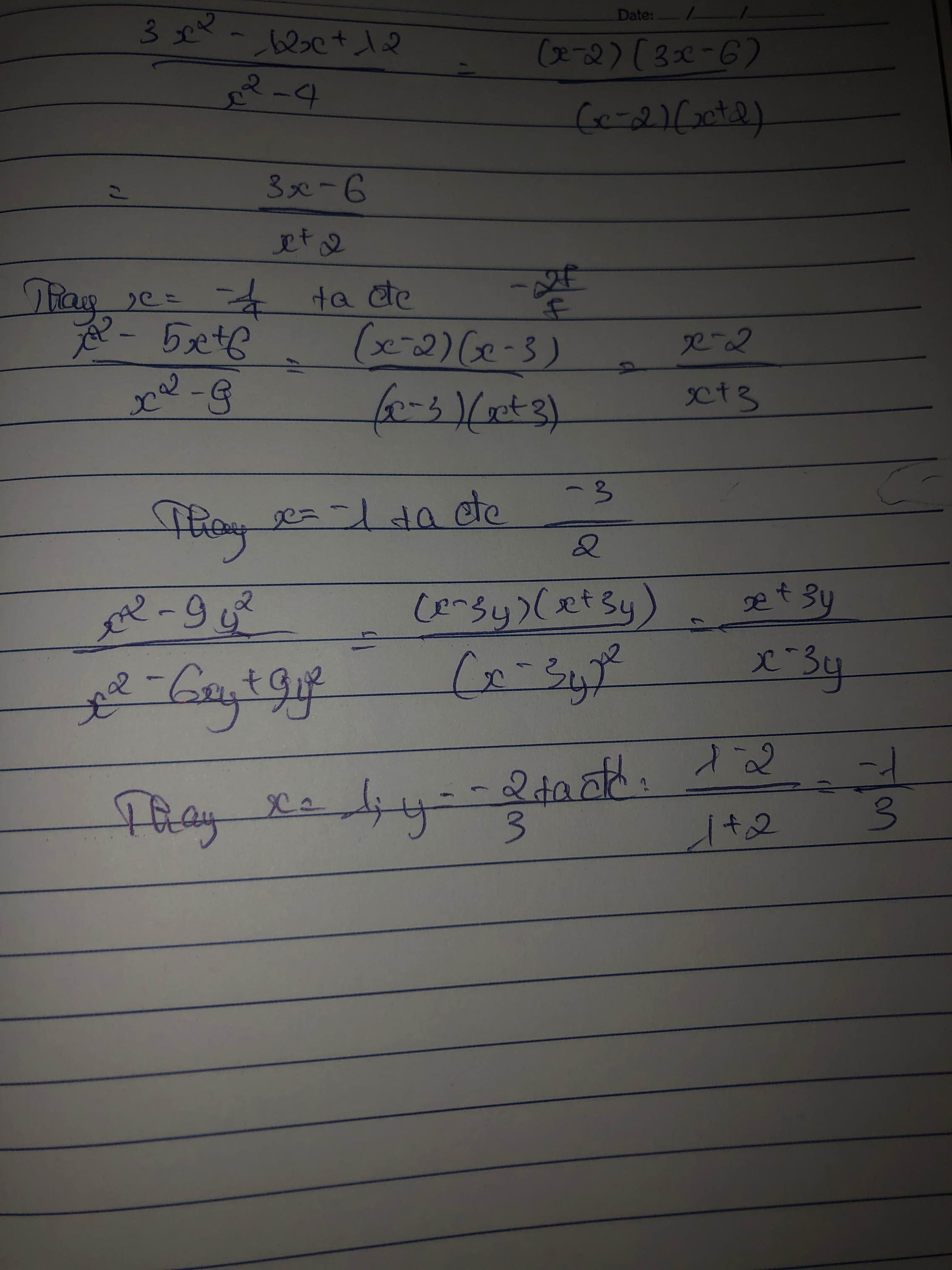A= x^2 + 9y^2 -6xy tại x=19 và y= 3

Những câu hỏi liên quan
1.Tính nhanh
a,x^2+9y^2-6xy tại x=16 và y=2
b,x^3-6x^2y+12xy^2-8y^3 tại x=14 và y=2
a) Ta có x2 + 9y2 - 6xy = (x - 3y)2 (1)
Thay x = 16 ; y = 2 vào (1) ta có
(x - 3y)2 = (16 - 2.3)2 = 102 = 100
b) Ta có x3 - 6x2y + 12xy2 - 8y3
= (x - 2y)3 (1)
Thay x = 14 ; y = 2 vào (1) ta có
(x - 2y)3 = (14 - 2.2)3 = 103 = 1000
a) \(x^2+9y^2-6xy=\left(x-3y\right)^2\)
Thay \(x=16;y=2\)vào biểu thức trên ta có :
\(\left(16-3.2\right)^2=\left(16-6\right)^2=10^2=100\)
Vậy tại x = 16 và y = 2 thì biểu thức trên = 100
b) \(x^3-6x^2y+12xy^2-8y^3=\left(x-2y\right)^3\)
Thay x = 14 và y = 2 vào biểu thức trên ta có :
\(\left(14-2.2\right)^3=\left(14-4\right)^3=10^3=1000\)
Vậy tại x = 14 và y = 2 thì biểu thức trên = 1000
\(a,x^2+9y^2-6xy\)
\(=x^2-6xy+9y^2\)
\(=\left(x-3y\right)^2\)
Tại x=16 và y=2 ta có:
\(\left(x-3y\right)^2=\left(16-3.2\right)^2=100\)
\(b,x^3-6x^2y+12xy^2-8y^3\)
\(=\left(x-2y\right)^3\)
Tại x=14 và y=2 ta có
\(\left(x-2y\right)^3=\left(14-2.2\right)^3=1000\)
rút gọn rồi tính giá trị biểu thức
\(\dfrac{x^2-9y^2}{x^2-6xy+9y^2}\) tại x=1, y=-\(\dfrac{2}{3}\)
\(\dfrac{x^2-9y^2}{x^2-6xy+9y^2}\) tại x = 1 , y = -\(\dfrac{2}{3}\)
= \(\dfrac{x^2-\left(3y\right)^2}{\left(x-3y\right)^2}\)
= \(\dfrac{\left(x-3y\right)\left(x+3y\right)}{\left(x-3y\right)}\)
= (x + 3y)
Thay x = 1 , y = -\(\dfrac{2}{3}\) vào
x + 3y
= 1 +3 . -\(\dfrac{2}{3}\)
= -1
Chúc bạn học tốt
Đúng 1
Bình luận (1)
tính giá trị biểu thức sau
x^2-6xy+9y^2 tại x=15 và y= -3
\(x^2-6xy+9y^2\)
\(=\left(x-3y\right)^2\)
\(=\left[15-3.\left(-3\right)\right]^2\)
\(=\left(15+9\right)^2\)
\(=24^2\)
\(=576\)
rút gọn rồi tính giá trị biểu thức
\(\dfrac{3x^2-12x+12}{x^2-4}\) tại x=\(-\dfrac{1}{4}\)
\(\dfrac{x^2-5x-6}{x^2-9}\) tại x=-1
\(\dfrac{x^2-9y^2}{x^2-6xy+9y^2}\) tại x=1, y=-\(\dfrac{2}{3}\)
a) Ta có: \(\dfrac{3x^2-12x+12}{x^2-4}\)
\(=\dfrac{3\left(x^2-4x+4\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)}{x+2}\)
\(=\dfrac{3\cdot\left(\dfrac{-1}{4}-2\right)}{\dfrac{-1}{4}+2}=-\dfrac{27}{7}\)
b) Ta có: \(\dfrac{x^2-5x-6}{x^2-9}\)
\(=\dfrac{\left(x-6\right)\left(x+1\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{\left(-1-6\right)\left(-1+1\right)}{\left(-1-3\right)\left(-1+3\right)}\)
=0
Đúng 0
Bình luận (0)
rút gọn rồi tính giá trị biểu thức
\(\dfrac{3x^2-12x+12}{x^2-4}\) tại x= -\(\dfrac{1}{4}\)
\(\dfrac{x^2-5x+6}{x^2-9}\) tại x= -1
\(\dfrac{x^2-9y^2}{x^2-6xy+9y^2}\) tại x=1, y =-\(\dfrac{2}{3}\)
Thu gọn rồi tính:
A=(x-5y)^2 +(2x-3y)^3 -(x-y)^3 -(2x+3y)(4x^2-6xy+9y^2)
Tại x=1/2 y=-1/2
giải hệ phương trình
\(\left\{{}\begin{matrix}2x^2+y^2=19\\x^2+9y^2=6xy\end{matrix}\right.\)
Từ pt dưới:
\(x^2+9y^2=6xy\Leftrightarrow x^2-6xy+9y^2=0\)
\(\Leftrightarrow\left(x-3y\right)^2=0\Leftrightarrow x-3y=0\Leftrightarrow x=3y\)
Thế lên pt trên: \(2.\left(3y\right)^2+y^2=19\)
\(\Leftrightarrow19y^2=19\Leftrightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=3\\y=-1\Rightarrow x=-3\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a, ptich da thuc thanh nhan tu : x(x-y) + 2(x-y)
b, tính nhanh gtbt x2 - 6xy + 9y2 tại x = 16 và y = 2
tick nha ạh
a, x(x-y)+2(x-y)=(x-y)(x+2)
b, \(x^2-6xy+9y^2=\left(x-3y\right)^2\)Thay x=16, y=2 có
\(x^2-6xy+9y^2=\left(x-3y\right)^2=\left(16-2\cdot3\right)^2=10^2=100\)
1) Chứng minh bt sau ko phụ thuộc vào biến
a) ( x-1)^ 3 - ( x+4) ( x^2- 4x+16) + 3x ( x-1)
b) (2x+3y) ( 4x^2- 6xy + 9y^2) - ( 2x - 3y ) ( 4x^2+ 6xy + 9y^2) - 27 ( 2y^3- 1 )
c) y( x^2- y^2) ( x^2+ y^2) - y( x^4- y^4)
d) ( x-1)^3- ( x-1) ( x^2+ x + 1 ) - 3 ( 1-x).x