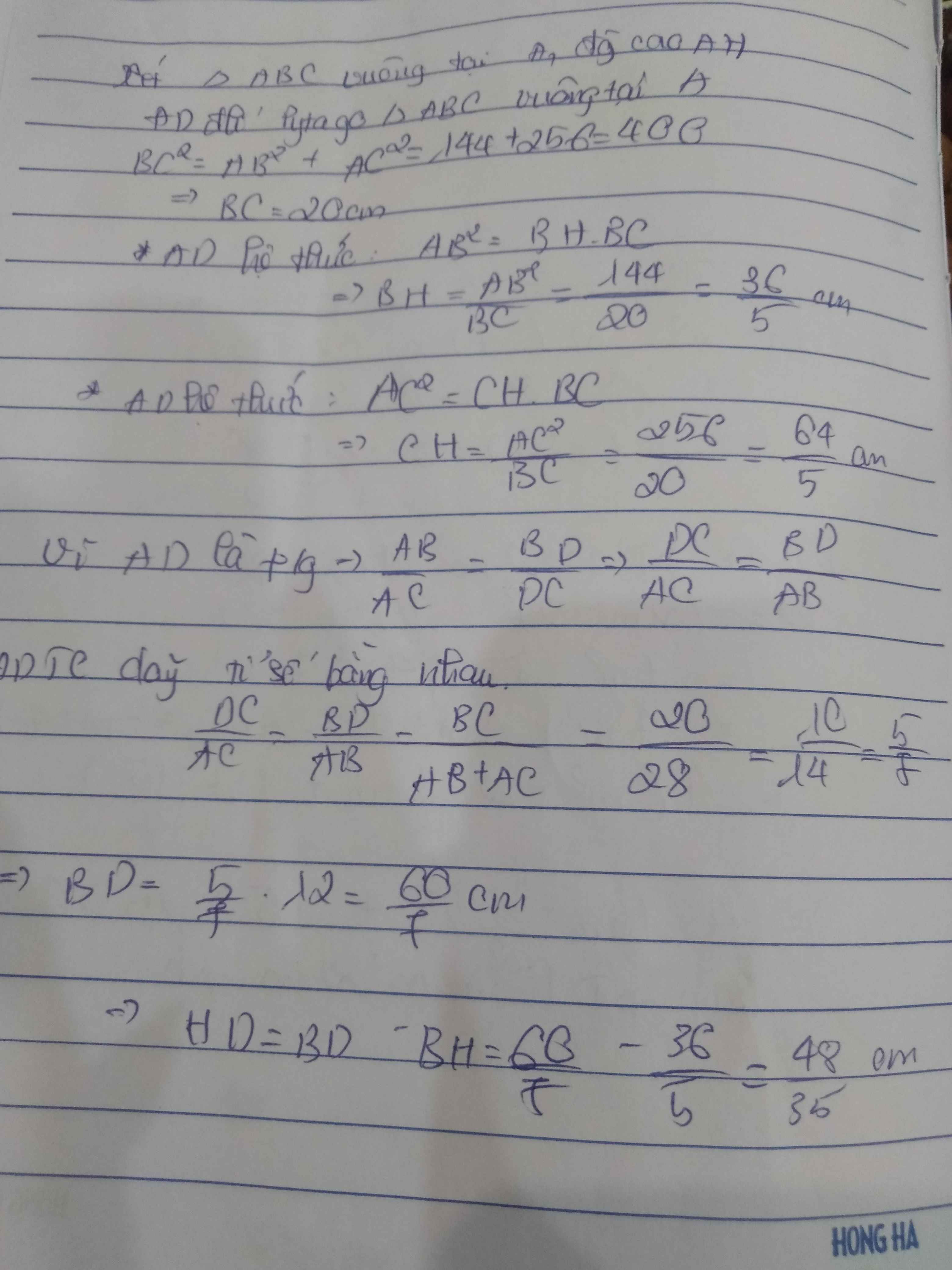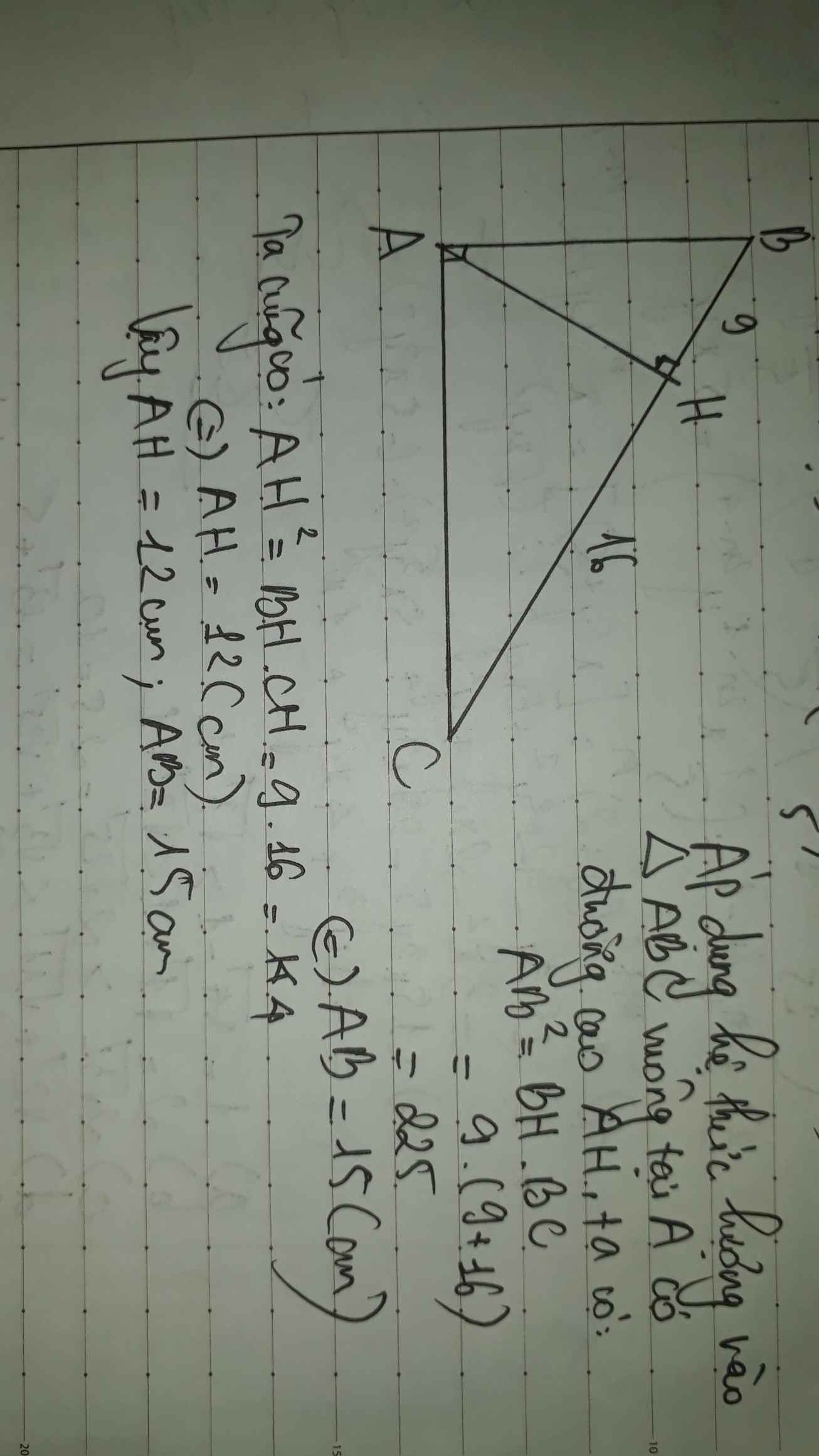AC^2=HC*CB

=>HC(HC+7,2)=16^2=256

=>HC^2+7,2*HC-256=0

=>HC=12,8cm

AH=căn 12,8*7,2=9,6cm

BC=12,8+7,2=20cm

AB=căn 7,2*20=12(cm)

AC=căn 12,8*20=16(cm)

Đặt BC=x \(\Rightarrow\)BH=x-16

\(\Rightarrow\)AB²=x(x-16) \(\Leftrightarrow\)15²=x(x-16) \(\Leftrightarrow\)x=25

\(\Rightarrow\)BC=25(cm),BH=25-16=9(cm)

AC=\(\sqrt{BC^2-AB^2}\)=20(cm)

AH=\(\sqrt{BH.HC}\)=12(cm

1) 

a) Xét ΔABC có 

\(BC^2=AC^2+AB^2\left(7.5^2=4.5^2+6^2\right)\)

nên ΔABC vuông tại A(Định lí Pytago đảo)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:

\(AB\cdot AC=AH\cdot BC\)

\(\Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{4.5\cdot6}{7.5}=\dfrac{27}{7.5}=3.6\left(cm\right)\)

Vậy: AH=3,6cm

b) Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:

\(AC^2=AH^2+CH^2\)

\(\Leftrightarrow CH^2=4.5^2-3.6^2=7.29\)

hay CH=2,7(cm)

Ta có: BH+CH=BC(H nằm giữa B và C)

nên BH=BC-CH=7,5-2,7=4,8(cm)

Vậy: BH=4,8cm; CH=2,7cm

1.a)Ta có:7,5²=4,5²+6² nên theo định lí Py-ta-go 

=>\(\Delta ABC\) vuông tại A

Ta có: AB.AC=BC.AH

=> \(AH=\dfrac{AC.AB}{BC}=\dfrac{4,5.6}{7,5}=3.6\)  (cm)

b)Ta có:AB²=BC.BH

  \(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{7,5}=4,8\) (cm)

Ta có:BH+CH=BC

     =>CH=BC-BH=7,5-4,8=2,7 (cm)

Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
(HC tự tính nha)

a ) Ta có : \(AH^2=BH.HC\)

\(\Rightarrow HC=\frac{AH^2}{BH}=\frac{24^2}{16}=36\left(cm\right)\)

Ta có : \(BC=BH+HC=16+36=52\left(cm\right)\)

\(\Rightarrow AB^2=BC.BH\)

\(AB^2=52.16\)

\(AB=\sqrt{52.16}\)

\(AB=\sqrt{52}.4\)

\(AB=28,8\left(cm\right)\)

\(\Rightarrow AC^2=BC.HC\)

\(AC^2=52.36\)

\(AC=\sqrt{52.36}\)

\(AC=\sqrt{52}.6\)

\(AC=43,3\left(cm\right)\)

b ) Ta có : \(sin\) \(B=\frac{AC}{BC}=\frac{43,3}{52}=0,83\)

\(\Rightarrow\widehat{B}=56^0\)

\(\Rightarrow\widehat{C}=\widehat{A}-\widehat{B}=90^0-56^0=34^0\).

Bài 2: 

Ta có: \(\dfrac{HB}{HC}=\dfrac{1}{3}\)

nên HC=3HB

Ta có: \(AH^2=HB\cdot HC\)

\(\Leftrightarrow HB^2=48\)

\(\Leftrightarrow HB=4\sqrt{3}\left(cm\right)\)

\(\Leftrightarrow BC=4\cdot HB=16\sqrt{3}\left(cm\right)\)

Bài 1:

ta có: \(AB=\dfrac{1}{2}AC\)

\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{1}{4}\)

\(\Leftrightarrow HC=4HB\)

Ta có: \(AH^2=HB\cdot HC\)

\(\Leftrightarrow HB=1\left(cm\right)\)

\(\Leftrightarrow HC=4\left(cm\right)\)

hay BC=5(cm)

Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=HC\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)