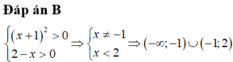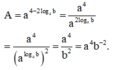Rút gọn (a-1)(b-1) - (a+1)(b+1) =0

Những câu hỏi liên quan
Rút gọn: a) A= √(3-√5) - √(3+√5). b) B=[√a/√(√a+1) - 1/√(a-√a)] : √(a+1)/a (với a>0, a khác 0)
`A=sqrt{3-sqrt5}-sqrt{3+sqrt5}`
`<=>sqrt2A=sqrt{6-2sqrt5}-sqrt{6+2sqrt5}`
`<=>sqrt2A=sqrt{(sqrt5-1)^2}-sqrt{(sqrt5+1)^2}`
`<=>sqrt2A=sqrt5-1-sqrt5-1=-2`
`<=>A=-sqrt2`
Câu b đề sai sai kiểu gì ý `sqrt{a+1}/a` là sao ;-;?
Đúng 2
Bình luận (0)
cho (1)/(a)+(1)/(b)+(1)/(c)=0 rút gọn M=(b+c)/(a)+(c+a)/(b)+(a+b)/(c)
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
\(\Leftrightarrow\frac{bc+ac+ba}{abc}=0\Leftrightarrow bc+ac+ba=0\Leftrightarrow c.\left(a+b\right)=-ba\Leftrightarrow a+b=\frac{-ab}{c}\)
\(b+c=-\frac{bc}{a},a+c=\frac{-ac}{b}\)
thay vô là đc :") lazzy~~
Đúng 0
Bình luận (0)
a√a +1 /√a +1 ( với a>=0) a,rút gọn A b, chứng minh a>= √a
a,Rút gọn: B = \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\) vs a≥0, a≠1.
b,GPT: \(2x^2-5x+2\)= 0
a) Ta có: \(B=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
=1-a
Đúng 0
Bình luận (0)
b) Ta có: \(2x^2-5x+2=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{1}{2};2\right\}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức
A
a
4
-
2
log
a
b
(
a
0
;
a
≠
1
;
b
0
)
A. B. C. D.
Đọc tiếp
Rút gọn biểu thức A = a 4 - 2 log a b ( a > 0 ; a ≠ 1 ; b > 0 )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Rút gọn biểu thức
A
a
4
-
2
log
a
b
a
0
;
a
≠
1
;
b
0
A.
a
2...
Đọc tiếp
Rút gọn biểu thức A = a 4 - 2 log a b a > 0 ; a ≠ 1 ; b > 0
A. a 2 b - 2
B. a 4 b - 2
C. a 2 b 2
D. a 4 b 2
Rút gọn biểu thức
P
a
3
b
3
-
1
3
-
1
.
a
-
1...
Đọc tiếp
Rút gọn biểu thức P = a 3 b 3 - 1 3 - 1 . a - 1 - 3 b - 2 a , b > 0
A. a 3
B. a - 2
C. a 2
D. a
Rút gọn biểu thức
P
a
3
b
3
-
1
3
+
1
.
a
-
1...
Đọc tiếp
Rút gọn biểu thức
P = a 3 b 3 - 1 3 + 1 . a - 1 - 3 b - 2 a , b > 0
![]()
![]()
![]()
![]()
Cho biểu thức
A=a+b-√ab/a√a+b√b - √a-√b-1/a-b
( với a>0,b>0,a khác b)
a) Rút gọn b+a
b) Tính giá trị của A biết a-b=1
a: \(A=\dfrac{1}{\sqrt{a}+\sqrt{b}}-\dfrac{\sqrt{a}-\sqrt{b}-1}{a-b}\)
\(=\dfrac{\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}+1}{a-b}=\dfrac{1}{a-b}\)
b: Khi a-b=1 thì A=1/1=1
Đúng 0
Bình luận (0)
cho a+b+c=0 rút gọn a=1/a^2+b^2-c^2+1/a^2+c^2-b^2+1/b^2+c^2-a^2