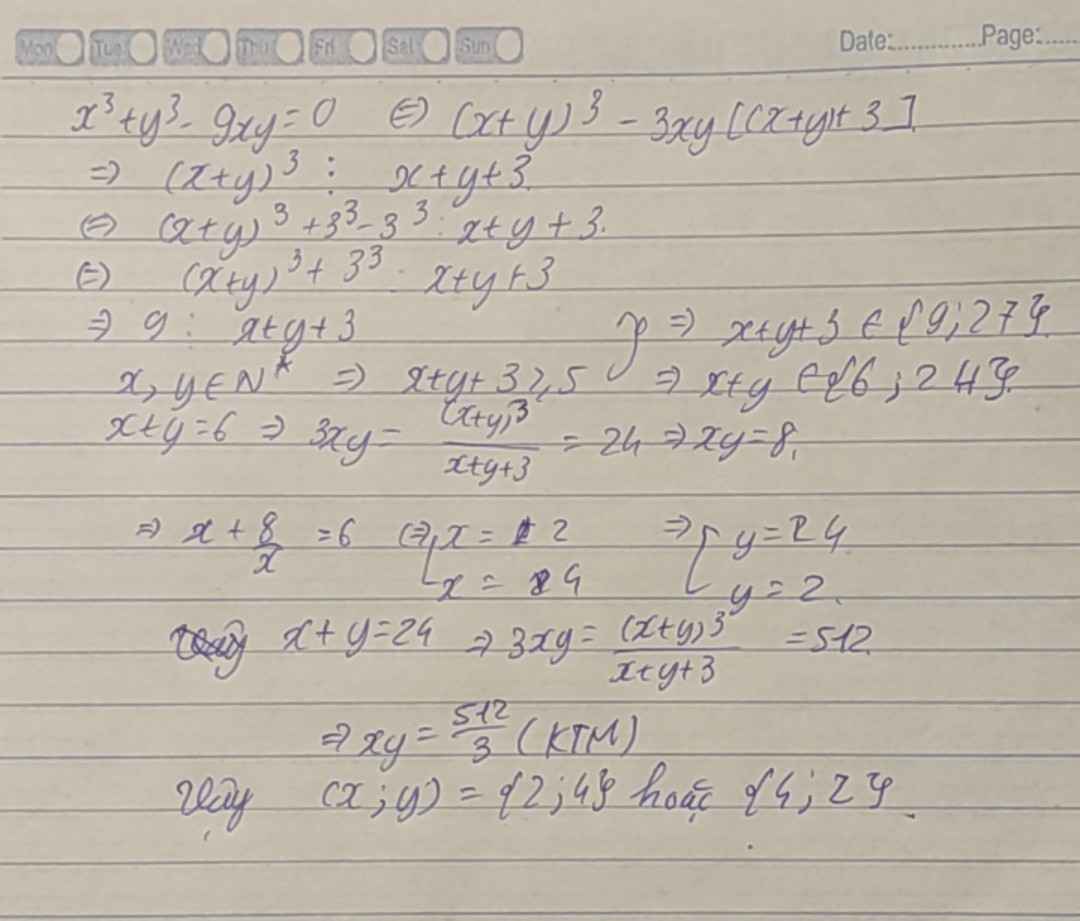Giaỉ phương trình nghiệm nguyên: a)\(x^3+y^3+1=6xy\) b)\(x^3-y^3+9xy=1\)

Những câu hỏi liên quan
Giải phương trình nghiệm nguyên
x3+y3=6xy-3
Giải phương trình nghiệm dương: \(x^3+y^3-9xy=0\).
Giaỉ phương trình nghiệm nguyên:(x2+y)(x+y2)=(x-y)3
Lưu ý:Sử dụng denta hoặc denta phẩy
Giaỉ hệ phương trình sau bằng phương pháp thếa)dfrac{1}{x}+dfrac{1}{y}dfrac{1}{2};dfrac{3}{x}-dfrac{4}{y}-1b)dfrac{3}{2x-y}-dfrac{6}{x+y}-1;dfrac{1}{2x-y}-dfrac{1}{x+y}0c)dfrac{5x}{x+1}+dfrac{y}{y-3}27;dfrac{2x}{x+1}-dfrac{3y}{y-3}4d)dfrac{7}{x+2}+dfrac{3}{y}2;dfrac{4}{x+2}-dfrac{1}{y}dfrac{5}{2}e)dfrac{2x}{x+4}+dfrac{2y}{2y-3}27;dfrac{2x}{x+4}-dfrac{6y}{2y-3}4Bạn nào biết thì giải giúp mình với ạ,mình xin cảm ơn ạ!!!
Đọc tiếp
Giaỉ hệ phương trình sau bằng phương pháp thế
a)\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2};\dfrac{3}{x}-\dfrac{4}{y}=-1\)
b)\(\dfrac{3}{2x-y}-\dfrac{6}{x+y}=-1;\dfrac{1}{2x-y}-\dfrac{1}{x+y}=0\)
c)\(\dfrac{5x}{x+1}+\dfrac{y}{y-3}=27;\dfrac{2x}{x+1}-\dfrac{3y}{y-3}=4\)
d)\(\dfrac{7}{x+2}+\dfrac{3}{y}=2;\dfrac{4}{x+2}-\dfrac{1}{y}=\dfrac{5}{2}\)
e)\(\dfrac{2x}{x+4}+\dfrac{2y}{2y-3}=27;\dfrac{2x}{x+4}-\dfrac{6y}{2y-3}=4\)
Bạn nào biết thì giải giúp mình với ạ,mình xin cảm ơn ạ!!!
bài tập: cho hệ phương trình left{{}begin{matrix}x+my1mx+y1end{matrix}right. (m là tham số )a, Giaỉ hệ phương trình khi m1,m-1,m2b,Tìm m để hệ phương trình đã cho b.1, có nghiệm duy nhấtb.2,vô nghiệmb.3,có vô số nghiệm c,Tìm m để hệ có nghiệm duy nhất x+2y3 thankyou
Đọc tiếp
bài tập: cho hệ phương trình \(\left\{{}\begin{matrix}x+my=1\\\\mx+y=1\end{matrix}\right.\) (m là tham số )
a, Giaỉ hệ phương trình khi m=1,m=-1,m=2
b,Tìm m để hệ phương trình đã cho
b.1, có nghiệm duy nhất
b.2,vô nghiệm
b.3,có vô số nghiệm
c,Tìm m để hệ có nghiệm duy nhất \(x+2y=3\)
thankyou
Lời giải:
a) Khi $m=1$ thì HPT trở thành:
\(\left\{\begin{matrix} x+y=1\\ x+y=1\end{matrix}\right.\Leftrightarrow x+y=1\Leftrightarrow y=1-x\)
Khi đó, hệ có nghiệm $(x,y)=(a,1-a)$ với $a$ là số thực bất kỳ.
Khi $m=-1$ thì hệ trở thành:
\(\left\{\begin{matrix} x-y=1\\ -x+y=1\end{matrix}\right.\Rightarrow (x-y)+(-x+y)=2\Leftrightarrow 0=2\) (vô lý)
Vậy HPT vô nghiệm
Khi $m=2$ thì hệ trở thành: \(\left\{\begin{matrix} x+2y=1\\ 2x+y=1\end{matrix}\right.\Rightarrow (x+2y)-(2x+y)=1-1=0\Leftrightarrow y-x=0\Leftrightarrow x=y\)
Thay $x=y$ vào 1 trong 2 PT của hệ thì có: $3x=3y=1\Rightarrow x=y=\frac{1}{3}$Vậy........
b)
PT $(1)\Rightarrow x=1-my$. Thay vào PT $(2)$ có:
$m(1-my)+y=1\Leftrightarrow y(1-m^2)=1-m(*)$
b.1
Để HPT có nghiệm duy nhất thì $(*)$ có nghiệm $y$ duy nhất
Điều này xảy ra khi $1-m^2\neq 0\Leftrightarrow (1-m)(1+m)\neq 0$
$\Leftrightarrow m\neq \pm 1$
b.2 Để HPT vô nghiệm thì $(*)$ vô nghiệm $y$. Điều này xảy ra khi $1-m^2=0$ và $1-m\neq 0$
$\Leftrightarrow m=-1$
b.3 Để HPT vô số nghiệm thì $(*)$ vô số nghiệm $y$. Điều này xảy ra khi $1-m^2=0$ và $1-m=0$
$\Leftrightarrow m=1$
c) Ở b.1 ta có với $m\neq \pm 1$ thì $(*)$ có nghiệm duy nhất $y=\frac{1}{m+1}$
$x=1-my=\frac{1}{m+1}$
Thay vào $x+2y=3$ thì:
$\frac{3}{m+1}=3\Leftrightarrow m=0$
Đúng 3
Bình luận (0)
Nhờ các bạn giải giùm mình 5 bài luôn nhé! Mình đang cần gấp lắm! Mình cảm ơn.1. Cho x,y,z khác 0 và (x+y+ z)^2 x^2+y^2+z^2.C/m 1/x^3 + 1/y^3 + 1/z^3 3/x*y*z.2. Giải phương trình:x^3 + 3ax^2 + 3(a^2 -bc)x +a^3+b^3 +c^3 (Ẩn x)3. Tìm nghiệm nguyên của phương trình:(x+y)^3(x-2)^3 + (y+2)^3 + 64. Tìm nghiệm nguyên dương thỏa mãn cả hai phương trình x^3 + y^3 + 3xyz z^3z^3(2x+2y)^3
Đọc tiếp
Nhờ các bạn giải giùm mình 5 bài luôn nhé! Mình đang cần gấp lắm! Mình cảm ơn.
1. Cho x,y,z khác 0 và (x+y+ z)^2 = x^2+y^2+z^2.
C/m 1/x^3 + 1/y^3 + 1/z^3= 3/x*y*z.
2. Giải phương trình:
x^3 + 3ax^2 + 3(a^2 -bc)x +a^3+b^3 +c^3
(Ẩn x)
3. Tìm nghiệm nguyên của phương trình:
(x+y)^3=(x-2)^3 + (y+2)^3 + 6
4. Tìm nghiệm nguyên dương thỏa mãn cả hai phương trình
x^3 + y^3 + 3xyz= z^3
z^3=(2x+2y)^3
tìm nghiệm nguyên tố của phương trình \(x^y+y^x+\left(x+y+1\right)^3=x^3+y^3+z+1\)
\(\Leftrightarrow x^y+y^x+x^3+y^3+1+3\left(x+y\right)\left(x+1\right)\left(y+1\right)=x^3+y^3+1+z\)
\(\Leftrightarrow x^y+y^x+3\left(x+y\right)\left(y+1\right)\left(x+1\right)=z\)
Do \(VT>3\Rightarrow z>3\Rightarrow z\) lẻ đồng thời z không chia hết cho 3
Nếu \(x;y\) đều lẻ hoặc đều chẵn \(\Rightarrow VT\) chẵn (không thỏa mãn)
\(\Rightarrow\) x và y có đúng 1 số chẵn, do vai trò của x; y như nhau, giả sử y chẵn \(\Rightarrow y=2\)
\(\Rightarrow x^2+2^x+9\left(x+2\right)\left(x+1\right)=z\)
- Nếu \(x>3\Rightarrow x^2\) chia 3 dư 1, đồng thời do x lẻ \(\Rightarrow x=2k+1\)
\(\Rightarrow2^x=2^{2k+1}=2.4^k\) chia 3 dư 2
\(\Rightarrow x^2+2^x\) chia hết cho 3 \(\Rightarrow VT\) chia hết cho 3 (không thỏa mãn)
\(\Rightarrow x\le3\Rightarrow x=3\Rightarrow z=197\) (thỏa mãn)
Vậy \(\left(x;y;z\right)=\left(3;2;197\right)\)
Đúng 0
Bình luận (0)
tìm nghiệm nguyên của phương trình sau :
a, x^3+y^3+z^3=1012
b, 7^z=2^x +3^y -1
c, 2^x * 3^y=1+5^z
Giaỉ các bất phương trình sau rồi biểu diễn tập nghiệm trên trục số
a) 2x+3>1-x b) 15-2(x-3) < -2x+5
c) (x+1)(x-3) ≤ (x+4) (x-1)
GIÚP mik nha mn
a: Ta có: \(2x+3>1-x\)
\(\Leftrightarrow3x>-2\)
hay \(x>-\dfrac{2}{3}\)
b: Ta có: \(15-2\left(x-3\right)< -2x+5\)
\(\Leftrightarrow15-2x+6+2x-5< 0\)
\(\Leftrightarrow16< 0\left(vôlý\right)\)
c: Ta có: \(\left(x+1\right)\left(x-3\right)\le\left(x+4\right)\left(x-1\right)\)
\(\Leftrightarrow x^2-3x+x-3-x^2+x-4x+4\le0\)
\(\Leftrightarrow-5x\le-1\)
hay \(x\ge\dfrac{1}{5}\)
Đúng 1
Bình luận (0)