Thực hiện phép nhân, rút gọn biểu thức:
(a-b)(b-c)(c-a).
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
1 thực hiện phép nhân
a, ( 2x^2 - 4x ) ( x - 1/2 )
b, ( x^2 - 2x + 1 ( x - 1 )
c, 3 ( y - x ) ( y^2 + xy + x^2 )
d, ( x - 1 ) ( x + 1 ) ( x - 2 )
2 rút gọn giá trị biểu thức ( dạng 2 : chứng tỏ biểu thức ko phụ thuộc vào giá trị của biến )
a, P = ( 2x + 1 ) ( 4x^2 - 2x + 1 ) tại x = 1/2
b, Q = ( X + 3y ) ( x^2 - 3xy + 9y^2 ) tại x = 1 và y = 1/3
3 chứng minh giá trị của biểu thức sau ko phụ thuộc vào giá trị của biến ( dạng 3 : tìm x biết x thỏa mãn điều kiện cho trc )
4 tìm x ( dạng 4 : chứng minh đẳng thức )
( 8x + 2 ) ( 1 - 3x ) + ( 6x - 1) ( 4x - 10 ) = -50
a. (2x2 - 4x)\(\left(x-\dfrac{1}{2}\right)\)
= 2x3 - x2 - 4x2 + 2
= 2x3 - 5x2 + 2
b. (x2 - 2x + 1)(x - 1)
= (x - 1)2(x - 1)
= (x - 1)3
c. 3(y - x)(y2 + xy + x2)
= 3(y3 - x3)
= 3y3 - 3x3
d. (x - 1)(x + 1)(x - 2)
= (x2 - 1)(x - 2)
= x3 - 2x2 - x + 2x
= x3 - 2x2 + x
= x3 - x2 - x2 + x
= x2(x - 1) - x(x - 1)
= (x2 - x)(x - 1)
= x(x - 1)(x - 1)
= x(x - 1)2
a, Thực hiện phép tính A = 7 - 4 3 + 1 2 - 3
b, Rút gọn biểu thức B = sin 2 19 0 + cos 2 19 0 + tan 19 0 - c o t 71 0
a, A = 7 - 4 3 + 1 2 - 3 = 2 - 3 + 2 + 3 = 4
b, B = sin 2 19 0 + cos 2 19 0 + tan 19 0 - c o t 71 0
= sin 2 19 0 + cos 2 19 0 + tan 19 0 - tan 19 0 = 1
1. Phân tích đa thức thành nhân tử
(a - b) (5x + 3) + 2(a - b)
2. Thực hiện phép tính
a) 3x2 (x - 1)
b) (2x + 3)2 - 4 (x - 3) (x + 3)
3. Rút gọn biểu thức
B= \(\dfrac{2X^3-4X^2+2X}{3X^2-3X}\)
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.
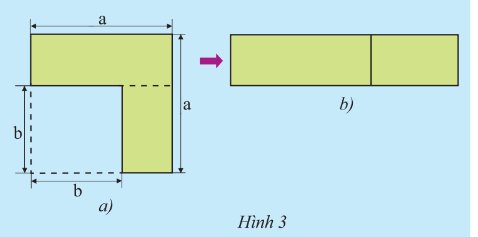
b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
a) Diện tích Hình 3a là: \({a^2} - {b^2}\)
Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)
b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)
Vậy diện tích của hai hình bằng nhau.
ĐỀ 1
Bài 1: (3,0 điểm)
1. Thực hiện các phép tính:
a) ![]()
![]()
2. Không dùng máy tính và bảng số hãy so sánh: 5 và ![]()
Bài 2: (3,0 điểm) Rút gọn các biểu thức sau:
a) ![]()
b) ![]()
c) 
Bài 3: (3,5 điểm)
Cho biểu thức  với x ³ 0 và x ¹ 1.
với x ³ 0 và x ¹ 1.
a) Chứng minh: 
b) Tính giá trị của A khi ![]()
c) Tìm các giá trị của x sao cho 
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức:
B =  với x > 2017
với x > 2017
Thực hiện phép nhân, rút gọn rồi tính giá trị của biểu thức:
a) x(x-y) +y (x+y) tại x= -6 y=8
x(x-y) + y(x+y)
=x(x-y) -y(x-y)
=(x-y)(x-y)
=(x-y)^2
=616
a) x(x – y) + y (x + y) = x2 – xy +yx + y2= x2+ y2
với x = -6, y = 8 biểu thức có giá trị là (-6)2 + 82 = 36 + 64 = 100
Thực hiện phép tính (rút gọn biểu thức)
a)\(\left(\sqrt{3}-2\right)\sqrt{7+4\sqrt{3}}\)
b) \(\sqrt{6+\sqrt{32}}\) - \(\sqrt{11-\sqrt{72}}\)
c) \(\sqrt{21-4\sqrt{5}}\) + \(\sqrt{21+4\sqrt{5}}\)
a: \(=\left(\sqrt{3}-2\right)\cdot\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\)
=3-4=-1
b: \(=\sqrt{6+4\sqrt{2}}-\sqrt{11-2\sqrt{18}}\)
\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=2+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}-1\)
c: \(=\sqrt{\left(2\sqrt{5}-1\right)^2}+\sqrt{\left(2\sqrt{5}+1\right)^2}\)
\(=2\sqrt{5}-1+2\sqrt{5}+1\)
\(=4\sqrt{5}\)
Thực hiện phép tính ( rút gọn biểu thức )
a) \(\dfrac{1}{2\sqrt{2}-3}\)+\(\dfrac{1}{2\sqrt{2}+3}\) b) \(\dfrac{\sqrt{2}}{2\sqrt{2}+\sqrt{7}}\)+\(\dfrac{\sqrt{2}}{2\sqrt{2}-\sqrt{7}}\)
c) \(\dfrac{1}{2-\sqrt{5}}\)-\(\dfrac{2}{2+\sqrt{5}}\)
a: \(=\dfrac{2\sqrt{2}+3+2\sqrt{2}-3}{8-9}\)
\(=\dfrac{4\sqrt{2}}{-1}=-4\sqrt{2}\)
b: \(=\dfrac{\sqrt{2}\left(2\sqrt{2}-\sqrt{7}\right)+\sqrt{2}\left(2\sqrt{2}+\sqrt{7}\right)}{8-7}\)
\(=4-\sqrt{14}+4+\sqrt{14}=8\)
c: \(=\dfrac{2+\sqrt{5}-2\left(2-\sqrt{5}\right)}{-1}=\dfrac{2+\sqrt{5}-4+2\sqrt{5}}{-1}\)
\(=-3\sqrt{5}+2\)
Thực hiện phép tính ( rút gọn biểu thức )
a) \(\dfrac{\sqrt{2}}{2\sqrt{2}-3}\)+\(\dfrac{1}{3+2\sqrt{2}}\) b) \(\dfrac{1}{\sqrt{10}+\sqrt{6}}\)+\(\dfrac{1}{\sqrt{6}-\sqrt{10}}\)
c) \(\dfrac{-2}{3\sqrt{8}}\)+\(\dfrac{1}{3-2\sqrt{2}}\)
a: \(=\dfrac{\sqrt{2}\left(2\sqrt{2}+3\right)+2\sqrt{2}-3}{-1}\)
\(=\dfrac{4+3\sqrt{2}+2\sqrt{2}-3}{-1}=-1-5\sqrt{2}\)
b: \(=\dfrac{1}{\sqrt{10}+\sqrt{6}}-\dfrac{1}{\sqrt{10}-\sqrt{6}}\)
\(=\dfrac{\sqrt{10}-\sqrt{6}-\sqrt{10}-\sqrt{6}}{4}=\dfrac{-2\sqrt{6}}{4}=-\dfrac{\sqrt{6}}{2}\)
c: \(\dfrac{-2}{3\sqrt{8}}+\dfrac{1}{3-2\sqrt{2}}\)
\(=\dfrac{-2\left(3-2\sqrt{2}\right)+6\sqrt{2}}{6\sqrt{2}\left(3-2\sqrt{2}\right)}=\dfrac{-6+4\sqrt{2}+6\sqrt{2}}{6\sqrt{2}\left(3-2\sqrt{2}\right)}\)
\(=\dfrac{10\sqrt{2}-6}{6\sqrt{2}\left(3-2\sqrt{2}\right)}=\dfrac{10-3\sqrt{2}}{6\left(3-2\sqrt{2}\right)}=\dfrac{18+11\sqrt{2}}{6}\)