Cho sin2α = a. Tính cos4α - sin4α
Những câu hỏi liên quan
cm đẳng thức
c) sin4α + cos4α - sin6α - cos6α = sin2α . cos2α
Ta có:
`sin^4 \alpha + cos^4 \alpha -sin^6 \alpha- cos^6\alpha`
`=sin^4\alpha+cos^4\alpha-(sin^2\alpha+cos^2\alpha)(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^4\alpha + cos^4\alpha-(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^2\alpha cos^2\alpha(ĐPCM)`
Đúng 1
Bình luận (0)
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:47
Cho góc bất kì α. Chứng minh các đẳng thức sau:
a) (sinα+cosα)2=1+sin2α;
b) cos4α−sin4α=cos2α.
a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)
Đúng 0
Bình luận (0)
Thu gọn biểu thức
a)1 - sin2α
b)(1 - cosα).(1 + cosα)
c)1 + sin2α + cos2α
d)sin4α + cos4α + 2.sin2α.cos2α
e)tan2α - sin2α.tan2α
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trịcủa các góc nhọn α.a) A cos4α + 2cos2α . sin2α + sin4ab) B sin4α + cos2α . sin2α + cos2αc) C 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos αd) D (tan α - cot α )2 - (tan α + cot α )2e) E 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)f) F dfrac{1}{1+sintext{α}}+dfrac{1}{1-sintext{α}}-2 tan2α
Đọc tiếp
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
6. CM đẳng thức
a) \(\dfrac{sin^3\alpha+cos^3\alpha}{sin\alpha+cos\alpha}=1-sin\alpha.cos\alpha\)
c) sin4α + cos4α - sin6α - cos6α = sin2α . cos2α
b) \(\dfrac{sin^2\alpha-cos^2\alpha}{1+2sin\alpha.cos\alpha}=\dfrac{tan\alpha-1}{tan\alpha+1}\)
a: \(VT=\dfrac{\left(sina+cosa\right)^3-3\cdot sina\cdot cosa\left(sina+cosa\right)}{sina+cosa}\)
=(sina+cosa)^2-3*sina*cosa
=sin^2a+cos^2a-sina*cosa
=1-sina*cosa=VP
c: VT=(sin^2a+cos^2a)^2-2*sin^2a*cos^2a-(sin^2a+cos^2a)^3+3*sin^2a*cos^2a*(sin^2a+cos^2a)
=1-2sin^2a*cos^2a-1+3*sin^2a*cos^2a
=sin^2a*cos^2a=VP
Đúng 0
Bình luận (0)
Cho A= Sin4α(1+2Cos2α)+Cos4α(1+2Sin2α)
Rút gọn A
\(A=sin^4a+2\cdot sin^4a\cdot cos^2a+cos^4a+2\cdot cos^4a\cdot sin^2a\)
\(=\left(sin^4a+cos^4a\right)+2\cdot sina^2a\cdot cos^2a\left(sin^2a+cos^2a\right)\)
\(=sin^4a+cos^4a+2\cdot sin^2a\cdot cos^2a\)
\(=\left(sin^2a+cos^2a\right)^2=1\)
Đúng 1
Bình luận (0)
Biết sinα + cosα = m. Tính sinα.cosα và | sin 4 α - cos 4 α |.
Ta có (sinα + cosα ) 2 = sin 2 α + 2sinαcosα + cos 2 α = 1 + 2sinαcosα
Mặt khác sinα + cosα = m nên sinα + cosα = m ⇔ (sinα + cosα ) 2 = m 2
⇔ sin 2 α + cos 2 α + 2sinαcosα = m 2
⇔ 1 + 2sinαcosα = m 2
⇔ 2sinαcosα = m 2 - 1
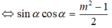
Đặt A = |sin4 α - cos 4 α |.
Ta có:
A = | sin 4 α - cos4α |
= |( sin 2 α - cos 2 α )( sin 2 α + cos 2 α )|
=|(sinα + cosα )(sinα - cosα )|
⇒ A 2 = (sinα + cosα ) 2 (sinα - cosα ) 2 = (1 + 2sinxcosx)(1 - 2sinxcosx)
⇒ A 2 = (1 + 2sinxcosx)(1 - 2sinxcosx )
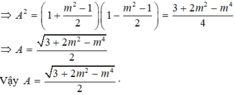
Đúng 0
Bình luận (0)
sin4α+cos4α+2sin2α.cos2α
\(\left(sin^2\alpha\right)^2+\left(cos^2\alpha\right)^2+2.sin\alpha.cos\alpha\\ =\left(sin^2\alpha+cos^2\alpha\right)^2\\ =\left(1\right)^2=1\)
Đúng 1
Bình luận (1)
\(\sin^4\alpha+2\cdot\sin^2\alpha\cdot\cos^2\alpha+\cos^4\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2\)
=1
Đúng 1
Bình luận (0)
M.n cho mik hỏi cách chứng minh ạ cos4α−sin4αcos2α
Đọc tiếp
M.n cho mik hỏi cách chứng minh ạ
cos4α−sin4α=cos
2α
cos^4a-sin^4a
=(cos^2a-sin^2a)(cos^2a+sin^2a)
=cos^2a-sin^2a
=cos2a
Đúng 0
Bình luận (0)
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
B = 4 ( sin 4 α + sin 4 α ) - cos 4 α
A = 4 [ ( sin 2 α + cos 2 α ) 2 - 2 sin 2 α cos 2 α ] - cos4α
= 4 ( 1 - sin 2 2 α / 2 ) - 1 + 2 sin 2 2 α = 3
Đúng 0
Bình luận (0)