Cho chóp SABCD có đáy là hv cạnh a, SA vuông vs đáy và SA bằng a. Tinh d(A,SBD)
Cho chóp SABCD có đáy là hv cạnh a, SA vuông vs đáy và SA bằng 2a a. Tính d(A,(SBC)) -> d (D, (SBC)) b. Tính d(A,(SBD)) -> d(C,(SBD))
a.
Từ A kẻ \(AH\perp SB\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng trong tam giác vuông SAB:
\(AH=\dfrac{SA.AB}{SB}=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
Do \(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=d\left(D;\left(SBC\right)\right)\)
\(\Rightarrow d\left(D;\left(SBC\right)\right)=\dfrac{2a\sqrt{5}}{5}\)
b.
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\) (t/c hình vuông)
Từ A kẻ \(AK\perp SO\) (1)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BO\Rightarrow BO\perp\left(SAO\right)\)
\(\Rightarrow BO\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SBD\right)\) \(\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông SAO:
\(AK=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
Do \(\left\{{}\begin{matrix}AC\cap\left(SBD\right)=O\\AO=CO\end{matrix}\right.\) \(\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)=\dfrac{2a}{3}\)
Cho hình chóp SABCD đáy là hình vuông tâm O cạnh a. SA=a căn 3. SA vuông góc với đáy. Tính góc a)(SBD) và (ABCD) b)(SBD) và (SAB) c)(SBC) và (ABCD) d)(SCD) và (ABCD)
cho chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc vs đáy , SA=a căn 3 . a) TÍnh ( SD , (SAB)
b) ( SO , (SAB) )
c) (SA , (SBD) )
d) (SD , (SAC) )
a: (SC;(SAB))=(SC;SB)=góc BSC
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
\(SB=\sqrt{a^2+\left(a\sqrt{3}\right)^2}=2a\)
\(cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{4a^2+5a^2-a^2}{2\cdot2a\cdot a\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
=>góc BSC=27 độ
b: (SO;(SAB))=(SO;SK)(OK vuông góc AB tại K)
Xét ΔABC có OK//BC
nên OK/BC=AK/AB=AO/AC=1/2
=>OK=a/2; AK=1/2a
\(SK=\sqrt{SA^2+AK^2}=\sqrt{3a^2+\dfrac{1}{4}a^2}=\dfrac{a\sqrt{13}}{2}\)
\(SO=\sqrt{SA^2+AO^2}=\sqrt{3a^2+\dfrac{1}{2}a^2}=\dfrac{a\sqrt{14}}{2}\)
OK=a/2
\(cosOSK=\dfrac{SO^2+SK^2-OK^2}{2\cdot SO\cdot SK}=\dfrac{\dfrac{14}{4}a^2+\dfrac{13}{4}a^2-\dfrac{1}{4}a^2}{2\cdot\dfrac{a\sqrt{14}}{2}\cdot\dfrac{a\sqrt{13}}{2}}=\dfrac{\sqrt{182}}{14}\)
=>góc OSK=16 độ
c: (SA;SBD)=(SA;SO)(AO vuông góc BD) tại O
=góc ASO
\(SO=\sqrt{SA^2+AO^2}=\sqrt{3a^2+\dfrac{1}{2}a^2}=\dfrac{a\sqrt{14}}{2}\)
SA=a căn 3
AO=a*căn 2/2
\(cosASO=\dfrac{SA^2+SO^2-AO^2}{2\cdot SA\cdot SO}=\dfrac{\sqrt{42}}{7}\)
=>góc ASO=22 độ
cho hình chóp SABCD đáy là hình thoi cạnh a, SD=a căn 2, tam giác SAB cân tại S, SA=a, (SBD) vuông góc với đáy. Tính thể tích SABCD/a³ căn 2
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a ,SA vuông góc với đáy và SA = a √3 /3. Góc giữa( SBC) và( ABCD) bằng bao nhiêu
\(\left\{{}\begin{matrix}BC\perp SA\subset\left(SAB\right)\\BC\perp AB\subset\left(SAB\right)\end{matrix}\right.\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\left\{{}\begin{matrix}BC\perp SB\\BC\perp AB\\\left(SBC\right)\cap\left(ABCD\right)=BC\end{matrix}\right.\Rightarrow\left(\left(SBC\right),\left(ABCD\right)\right)=\widehat{SBA}\)
\(\tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{3.a}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SBA}=30^0\)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh bằng a có SA vuông góc với mặt phẳng đáy và SA = a\(\sqrt{3}\). Tính sin của góc giữa AC và (SBC).
Từ A kẻ \(AE\perp SB\) (\(E\in SB\))
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(SBC\right)\)
\(\Rightarrow\widehat{ACE}\) là góc giữa AC và (SBC)
Hệ thức lượng trong tam giác SAB:
\(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AE=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{3}}{2}\)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
\(\Rightarrow sin\widehat{ACE}=\dfrac{AE}{AC}=\dfrac{\sqrt{6}}{4}\)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB=1, AD=2 cạnh bên SA vuông góc với đáy và S A = 5 α là số đo góc giữa hai mặt phẳng (SAB) và (SBD), cosα
A. 145 29
B. 5 5
C. 6 6
D. 29 25
Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa SC và AD bằng 60 ° . Tính thể tích khối chóp SABCD bằng
A. 2 a 3 3
B. 3 a 3 3
C. 2 a 3 6
D. 2 2 a 3 3
Chọn A.
Phương pháp: Sử dụng kiến thức về góc giữa hai đường thẳng: “ Góc giữa hai đường thẳng trong không gian là góc giữa hai đường thẳng (khác) tương ứng song song (hoặc trùng) với hai đường thẳng đó. Từ đó sử dụng lượng giác và định lý
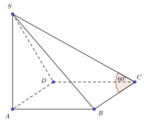
Pytago để tinh đường cao SA
Cách giải:

Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa SC và AD bằng 60 ° . Tính thể tích khối chóp SABCD bằng
![]()
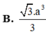
![]()
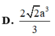
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên S A = a và vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt (SBD) bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3
Trong tam giác SOC, kẻ OK ⊥ OS(như hình vẽ).(1)
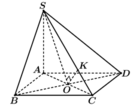
Dễ dàng chứng minh được ![]()
![]()
![]()
Ta tính được 
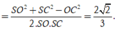
Chọn B.