Cho tam giác ABC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC)
a, Chứng minh: HB=HC và BAH=CAH
b, Tính độ dài AH
c, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
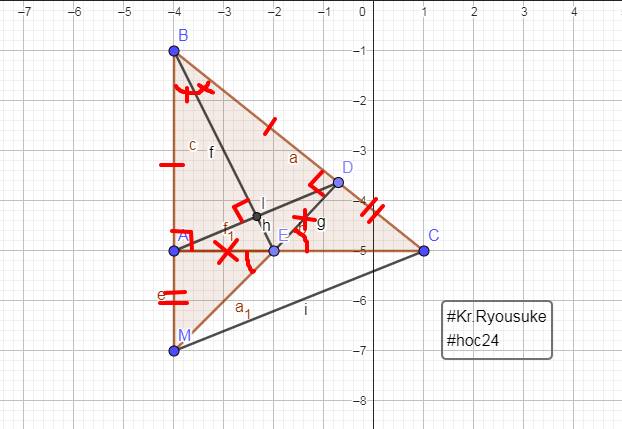
Bài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN
a, Chứng minh: tam giác ABM = tam giác ACN
b, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AH=AK
c, Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho tam giác ABC, kẻ BE vuông góc với AC và CF vuông góc với AB. Biết BE=CF=8 cm. Độ dài các đoạn thẳng BF và BC tỉ lệ với 3 và 5.
a, Chứng minh tam giác ABC là tam giác cân
b, Tính độ dài cạnh đáy BC
c, BE và CF cắt nhau tại O. Nối OA và EF. Chứng minh đường thẳng OA là trung trực của đoạn thẳng EF
Bài 5 : Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC (D thuộc AC). Từ D kẻ DE vuông góc với BC tại E. Gọi I là giao điểm của AE và BD. Chứng minh:
a, Tam giác ADB= tam giác EDB
b, BD là đường trung trực của AE
c, Tam giác EDC vuông cân
d, Lấy F thuộc tia đối của tia AB sao cho AF=EC.Chứng minh 3 điểm E, D, F thẳng hàng
Bài 6: Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm E, trên cạnh MP lấy điểm F sao cho ME=MF. Gọi S là giao điểm của NF và PE. Chứng minh
a, Tam giác MNF= tam giác MPE
b, Tam giác NSE= tam giác PSE
c, EF // NP
d, Lấy K là trung điểm của NP. Chứng minh ba điểm M, S, K thẳng hàng
Bài 7: Cho tam giác ABC vuông tại A. Trên BC lấy E sao cho BE=AB. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại D
a, Chứng minh AD=AE và góc ABD= góc EBD
b, Lấy điểm F thuộc tia đối của tia AB sao cho AF=EC. Chứng minh tam giác DFC cân
c, Gọi O là giao điểm của BD và AE. Chứng minh BD là đường trung trực của AE
d, Chứng minh 3 điểm F, D,E thẳng hàng
Mình đang cần gấp