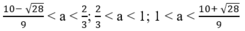a/Cho đồ thị (P):y=ax2.Xác định a biết rằng M(2;-2) thuộc đồ thị (P) rồi vẽ (P).Chứng tỏ rằng parabol đi qua điểm N(-4;-8) và không đi qua điểm E(6;-10)
b/Tìm những điểm trên parobol sao cho những điểm đó cách đều hai trục tọa độ
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 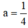
Vậy hàm số: 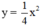
| x | -4 | -2 | 0 | 2 | 4 |
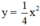 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
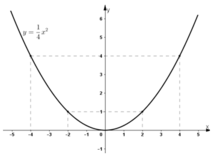
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 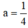
Vậy hàm số: 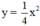
| x | -4 | -2 | 0 | 2 | 4 |
 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
Bài 12: a)Xác định hệ số a của hàm số y = ax2, biết rằng đồ thị hàm số đi qua điểm A(2;-1)
b) Vẽ đồ thị của hàm số đó
CÓ AI CÒN THỨC KO VẬYY
Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
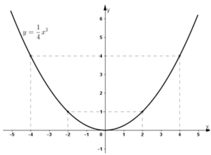
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:
Cho hàm số y = ax2 có đồ thị hàm số (P).1) xác định a biết (P) đi qua điểm A (1 ;- 2). 2) vẽ đồ thị (P). 3)Tìm điểm thuộc (P) có hoành độ bằng 2 4)Tìm điểm thuộc (P) có tung độ bằng -4
1) Để (P) đi qua điểm A(1;-2) thì
Thay x=1 và y=-2 vào hàm số \(y=ax^2\), ta được:
\(a\cdot1^2=-2\)
hay a=-2
giúp em với mọi người ơi
cho hàm số y=ax2-2x+C (P) xác định hàm số biết đồ thị (P)
A) đi qua A (1,0) và B (-2,15)
B) có đỉnh I (-1,4)
a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a-2+c=0\\4a+c+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+c=2\\4a+c=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-6\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\c=0\end{matrix}\right.\)
Cho hàm số y= ax2 (P) đi qua điểm A(1;2)
a) xác định a và vẽ đồ thị
b) cho đường thẳng y =-x+b cắt (P) tại A và B. Xác định b và tính toạ độ B
c) cho đường thẳng (d): y= mx-m2-\(\dfrac{3}{2}m-\dfrac{3}{4}\) . chứng minh (d) và (P) không cắt nhau với mọi m
(P): \(y=2x^2\)
Phương trình hoành độ giao điểm (P) và (d):
\(2x^2=mx-m^2-\dfrac{3}{2}m-\dfrac{3}{4}\)
\(\Leftrightarrow2x^2-mx+m^2+\dfrac{3}{2}m+\dfrac{3}{4}=0\) (1)
\(\Delta=m^2-8\left(m^2+\dfrac{3}{2}m+\dfrac{3}{4}\right)=-7m^2-12m-6=-7\left(m+\dfrac{6}{7}\right)^2-\dfrac{6}{7}< 0\) ; \(\forall m\)
\(\Rightarrow\) (1) vô nghiệm với mọi m hau (d) và (P) ko cắt nhau với mọi m
Cho hàm số y=ax2 (P) (a khác 0) đi qua điểm A(1;2)
a) xác gđịnh a và vẽ đồ thị hàm số vừa tìm dc
b) đường thẳng y= -x + b cắt (P) tại 2 điểm A và B. Xác định b và vẽ tọa độ điểm B
c) cho đường thẳng (d): y= mx - m2 - \(\dfrac{3}{2}\)m -\(\dfrac{3}{4}\). Chứng minh (d) và (P) không cắt nhau với mọi giá trị m
a) Thay x=1 và y=2 vào (P), ta được:
\(a\cdot1^2=2\)
hay a=2
cho hàm số : y=x^2; y=-x+2
a, Xác định tọa độ giao điểm A, B của đồ thị 2 hàm số đã cho và tọa độ trung điểm I của đoạn AB, biết rằng A có hoành độ dương
b, Xác định tọa độ của điểm M thuộc đồ thị hàm số y=x^2 sao cho tam giác ABM cân tại M
cho hàm số : y=x^2; y=-x+2 a, Xác định tọa độ giao điểm A, B của đồ thị 2 hàm số đã cho và tọa độ trung điểm I của đoạn AB, biết rằng A có hoành độ dương b, Xác định tọa độ của điểm M thuộc đồ thị hàm số y=x^2 sao cho tam giác ABM cân tại M
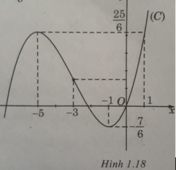
Cho hàm số y = a - 1 x 3 3 + ax 2 + 3 a - 2 x
Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.
Đồ thị cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình y = 0 có ba nghiệm phân biệt. Ta có
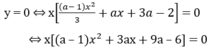
y = 0 có ba nghiệm phân biệt khi và chỉ khi phương trình
(a - 1) x 2 + 3ax + 9a - 6 = 0
Có hai nghiệm phân biệt khác 0. Muốn vậy, ta phải có
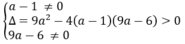
Giải hệ trên, ta được: