cho tam giác ABC có phương trình cạnh AB:5x-3y+2=0 và có phương trình hai đường cao AA':4x-3y+1=0,BB':7x+2y-22=0.Lập phương trình hai cạnh còn lại và đường cao CC' của tam giác ABC.

Những câu hỏi liên quan
cho tam giác ABC có phương trình đường thẳng chứa cạnh AB là 5x - 3y + 2 = 0,và các đường cao kể từ A,B lần lượt có phương trình 4x - 3y + 1 = 0 và 7x + 2y - 22 = 0. viết phương trình các cạnh còn lại của tam giác ABC
cho tam giác ABC có phương trình cạnh AB :5x-3y+2=0 ,các đường cao qua đỉnh A và B lần lượt là (d1):4x-3y+1=0 ;(d2):7x+2y-22=0 .Lập phương trình 2 cạnh AB và AC và đường cao thứ 3
A = AB giao d1=> Tọa độ A là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x+1=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x=-1\\y=\frac{1+4x}{3}\end{cases}\)<=> \(\begin{cases}x=-1\\y=-1\end{cases}\)=> A (-1; -1)
Đường thẳng d2 có vtpt là \(\vec{n_2}\left(7;2\right)\) chính là vtcp của đường thẳng AC , điểm A thuộc AC
=> Phương trình đường thẳng AC có dạng: \(\begin{cases}x=-1+7t\\y=-1+2t\end{cases}\)(t \(\in\) R)
Gọi H = d1 \(\cap\) d2 => tọa độ H là nghiệm của pt: \(\begin{cases}7x+2y-22=0\\4x-3y+1=0\end{cases}\) <=> \(\begin{cases}x=\frac{64}{29}\\y=\frac{95}{29}\end{cases}\)=> H (\(\frac{64}{29};\frac{95}{29}\))
Đường cao CH đi qua H và có vtcp chính là vtpt của AB là \(\vec{n}\) (5; -3)
=> Phương trình CH có dạng : \(\begin{cases}x=\frac{64}{29}+5t\\y=\frac{95}{29}-3t\end{cases}\)
B = AB \(\cap\) d2 => Tọa độ B là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\7x+2y-22=0\end{cases}\) <=> \(\begin{cases}x=2\\y=4\end{cases}\)=> B (2;4)
Đường thẳng BC đi qua B , có vtcp chính là vtpt của d1 là \(\vec{n_1}\)(4;-3)
=> phương trình đường thẳng BC là: \(\begin{cases}x=2+4t\\y=4-3t\end{cases}\)
Đúng 1
Bình luận (0)
A = AB giao d1=> Tọa độ A là nghiệm của hệ : {5x−3y+2=04x−3y+1=0{5x−3y+2=04x−3y+1=0<=> {x+1=04x−3y+1=0{x+1=04x−3y+1=0<=> {x=−1y=1+4x3{x=−1y=1+4x3<=> {x=−1y=−1{x=−1y=−1=> A (-1; -1)
Đường thẳng d2 có vtpt là →n2(7;2)n2→(7;2) chính là vtcp của đường thẳng AC , điểm A thuộc AC
=> Phương trình đường thẳng AC có dạng: {x=−1+7ty=−1+2t{x=−1+7ty=−1+2t(t ∈∈ R)
Gọi H = d1 ∩∩ d2 => tọa độ H là nghiệm của pt: {7x+2y−22=04x−3y+1=0{7x+2y−22=04x−3y+1=0 <=> {x=6429y=9529{x=6429y=9529=> H (6429;95296429;9529)
Đường cao CH đi qua H và có vtcp chính là vtpt của AB là →nn→ (5; -3)
=> Phương trình CH có dạng : {x=6429+5ty=9529−3t{x=6429+5ty=9529−3t
B = AB ∩∩ d2 => Tọa độ B là nghiệm của hệ : {5x−3y+2=07x+2y−22=0{5x−3y+2=07x+2y−22=0 <=> {x=2y=4{x=2y=4=> B (2;4)
Đường thẳng BC đi qua B , có vtcp chính là vtpt của d1 là →n1n1→(4;-3)
=> phương trình đường thẳng BC là: {x=2+4ty=4−3t
Đúng 0
Bình luận (0)
cho tgABC có pt cạnh AB là : 5x - 3y + 2 =0 và có 2 đường cao :
AA' : 4x - 3y + 1= 0
BB' : 7x + 2y -22 =0
lập phương trình 2 cạnh còn lại và dường cao CC' của tgABC
Cho tam giác ABC, biết phương trình một cạnh và hai đường cao. Viết phương trình hai cạnh và đường cao còn lại với
a, AB: 4x+y-12=0, BB': 5x-4y-15=0, CC': 2x+2y-9=0
b, BC: 5x-3y+2=0, BB': 4x-3y+1=0, CC': 7x+2y-22=0
c, BC: x-y+2=0, BB': 2x-7y-6=0, CC': 7x-2y-1=0
d, BC: 5x-3y+2=0, BB': 2x-y-1=0, CC': x+3y-1=0
4 câu làm tương tự nhau, nhưng câu a chắc bạn ghi nhầm đề (hoặc đề sai). Do \(AB\perp CC'\) nhưng \(4.2+1.2\ne0\) là hoàn toàn vô lý
Mình làm câu b, 2 câu còn lại bạn làm tương tự
Gọi H là trực tâm tam giác \(\Rightarrow\) H là giao điểm BB' và CC'
Tọa độ H là nghiệm \(\left\{{}\begin{matrix}4x-3y+1=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{64}{29};\frac{95}{29}\right)\)
B là giao điểm BC và BB' nên tọa độ B là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\4x-3y+1=0\end{matrix}\right.\) \(\Rightarrow B\left(-1;-1\right)\)
C là giao điểm BC và CC' nên tọa độ C là nghiệm:
\(\left\{{}\begin{matrix}5x-3y+2=0\\7x+2y-22=0\end{matrix}\right.\) \(\Rightarrow C\left(2;4\right)\)
Đường AA' đi qua H và vuông góc BC nên nhận \(\left(3;5\right)\) là 1 vtpt
Phương trình AA':
\(3\left(x-\frac{64}{29}\right)+5\left(x-\frac{95}{29}\right)=0\Leftrightarrow3x+5y-23=0\)
Đường thẳng AB qua B và vuông góc CC' nên nhận \(\left(2;-7\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-7\left(y+1\right)=0\Leftrightarrow2x-7y-5=0\)
Đường thẳng AC qua C và vuông góc BB' nên nhận \(\left(3;4\right)\) là 1 vtpt
Phương trình AC:
\(3\left(x-2\right)+4\left(y-4\right)=0\Leftrightarrow3x+4y-22=0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết phương trình ba cạnh của tam giác là AB: x – 3y – 1 0, BC: x + 3y + 7 0, CA: 5x – 2y + 1 0 Phương trình đường cao AH của tam giác là: A.13x – 39y + 9 0 B.39x – 13 y + 9 0 C.39x – 13y – 9 0 D.39x + 13y + 9 0
Đọc tiếp
Cho tam giác ABC, biết phương trình ba cạnh của tam giác là AB: x – 3y – 1 = 0, BC: x + 3y + 7 = 0, CA: 5x – 2y + 1 = 0 Phương trình đường cao AH của tam giác là:
A.13x – 39y + 9 = 0
B.39x – 13 y + 9 = 0
C.39x – 13y – 9 = 0
D.39x + 13y + 9 = 0
Ta có, AB và AC cắt nhau tại A nên tọa độ đỉnh A là nghiệm của hệ phương trình :
x − 3 y − 1 = 0 5 x − 2 y + 1 = 0 ⇒ A − 5 13 ; − 6 13
Đường thẳng BC có VTPT n B C → ( 1 ; 3 ) .
Vì A H ⊥ B C nên đường thẳng AH nhận vecto n B C → ( 1 ; 3 ) làm VTCP, một VTPT của AH là: n A H → ( 3 ; − 1 )
Phương trình đường cao AH của tam giác là:
3 x + 5 13 − y + 6 13 = 0 ⇔ 39 x − 13 y + 9 = 0
ĐÁP ÁN B
Đúng 1
Bình luận (0)
Cho tam giác ABC có phương trình các cạnh AB: x + y - 9 = 0, phương trình các đường cao qua đỉnh A là x + 2y - 13 = 0 (d1), qua B là 7x + 5y - 49 = 0 (d2). Lập phương trình cạnh AC, BC và đường cao còn lại
Cho tam giác ABC với H là trực tâm. Biết phương trình đường thẳng AB, BH và AH lần lượt là 4x + y – 12 = 0, 5x – 4y – 15 = 0 và 2x + 2y – 9 = 0. Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.
Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:
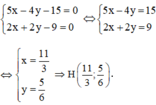
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:
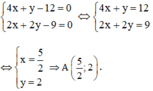
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:
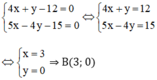
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua 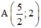
⇒ Phương trình đường thẳng AC: 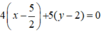 hay 4x + 5y – 20 = 0.
hay 4x + 5y – 20 = 0.
+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt
CH đi qua 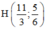
⇒ Phương trình đường thẳng CH: 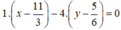 hay CH: 3x – 12y - 1 = 0.
hay CH: 3x – 12y - 1 = 0.
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.
Đúng 1
Bình luận (0)
Tam giác ABC có đỉnh A(-1; -3) . Phương trình đường cao BB’: 5x+ 3y -25= 0; phương trình đường cao
CC’: 3x+8y -12= 0. Toạ độ đỉnh B là
A. (5; 2)
B. (2; 5)
C.( 2; -5)
D. (-5; 2)
Đáp án B
Đường thẳng AB vuông góc với CC’ nên nhận u → (3; 8) làm VTCP và n → (8; -3) làm VTPT
Do đó d có phương trình: 8( x+ 1) -3( y+ 3) = 0 hay 8x- 3y -1= 0
Tọa độ điểm B là nghiệm của hệ phương trình
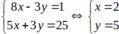
Đúng 0
Bình luận (0)
BÀI 1: cho tam giác ABC,biết pt 1 cạnh và hai đường cao.Viết PTTQ hai cạnh và đường cao còn lại,với
a, BC:4x+y-120;BB5x-4y+50;CC2x+2y-90
b, BC:5x-3y+20;BB:4x-3y+10;CC7x+2y-220
BÀI 2: cho tam giác ABC và tọa độ một đỉnh và phương trình đường cao.Viết phương trình các cạnh của tam giác đó với:
a, A(3,0),BB2x+2y-90;CC3x-12y-10
b,A(1,0), BBx-2y+10;CC3x+y-10
Đọc tiếp
BÀI 1: cho tam giác ABC,biết pt 1 cạnh và hai đường cao.Viết PTTQ hai cạnh và đường cao còn lại,với
a, BC:4x+y-12=0;BB'=5x-4y+5=0;CC'=2x+2y-9=0
b, BC:5x-3y+2=0;BB':4x-3y+1=0;CC'=7x+2y-22=0
BÀI 2: cho tam giác ABC và tọa độ một đỉnh và phương trình đường cao.Viết phương trình các cạnh của tam giác đó với:
a, A(3,0),BB'=2x+2y-9=0;CC'=3x-12y-1=0
b,A(1,0), BB'=x-2y+1=0;CC'=3x+y-1=0















